Direct Form 1
The most straightforward implementation is the Direct Form 1, which has the following difference equation:
or, if normalized:
Here the 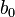 ,
,  and
and  coefficients determine zeros, and
coefficients determine zeros, and  ,
, 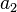 determine the position of the poles.
determine the position of the poles.
Flow graph of biquad filter in Direct Form 1:
Direct Form 2
The Direct Form 1 implementation requires four delay registers. An equivalent circuit is the Direct Form 2 implementation, which requires only two delay registers:
The Direct Form 2 implementation is called the canonical form, because it uses the minimal amount of delays, adders and multipliers, yielding in the same transfer function as the Direct Form 1 implementation. The difference equations for DF2 are:
where
//ASM example
/////////////////////////////////////////////////////////////
// //
// Process the audio stream //
// //
/////////////////////////////////////////////////////////////
#include <def21262.h>
#define SECTIONS 3 /* Number of second-order sections (biquads) */
.section /pm seg_pmco;
.global _Cascaded_IIR_Filter_SIMD;
.extern inbuf;
.extern outbuf;
.extern delaybuf;
.extern coefficients;
_Cascaded_IIR_Filter_SIMD:
/*****************************************************************************
The algorithm:
IIR Second order sections - The cannonic second-order section implemented as
"Direct Form II" biquads. Note that the SIMD architecture of the 2126x SHARC
family enables the two parallel execution units to filter the left and right
channel simultaneously. All register moves and memory reads implicitly apply
to the shadow processing element (PEy) as well as the primary computational
unit (PEx).
*****************************************************************************
Given the most general biquadratic (second order rational polynomial)
b0 + b1'*z^-1 + b2'*z^-2
H(z) = -------------------------- ,
a0 + a1'*z^-1 + a2'*z^-2
we may factor out the gain of the transfer function,
b0 (b1'/a0)*z^-1 + (b2'/a0)*z^-2
H(z) = ---- * -------------------------------
a0 (a1'/b0)*z^-1 + (a2'/b0)*z^-2
and normalize the coefficients, such that
a1*z^-1 + a2*z^-2
H(z) = A * -------------------
b1*z^-1 + b2*z^-2
where A = gain = b1'/a0
a1 = a1'/b0, a2 = a2'/b0, b1 = b1'/a0, b2 = b2'/a0
This leaves only four true filter coefficients. The gain values from
all of the sections may be combined into a single channel gain applied
apart from the inner computational loop. With the simplified coefficients,
the cannonic direct form II may be written as a pair of difference
equations:
w[n] = x[n] + a1*w[n-1] + a2*w[n-2]
y[n] = w[n] + b1*w[n-1] + b2*w[n-2]
which leads to the following pseudocode:
read(x[n])
f12=0, f2=w[n-1], read(a1)
--- Loop --------------------------------------------------------------------
f12=a1*w[n-1], f8=f8 + f12, f3=w[n-2], read(a2)
f12=a2*w[n-2], f8=x[n] + a1*w[n-2], w[n-1] -> w[n-2]', read(b1)
f12=b1*w[n-2], w[n]=x[n] + a1*w[n-2] + a2*w[n-1], f2=w[n-1], read(b2)
f12=b2*w[n-1], f8=w[n] + b1*w[n-2], w[n] -> w[n-1]', read(a1)
-----------------------------------------------------------------------------
y[n]=f8 + f12
**************************************************************************/
/* Subroutine that implements the pseudocode above */
cascaded_biquad:
bit set mode1 CBUFEN | PEYEN ; // Enable SIMD mode
b0 = delaybuf;
b1 = b0;
b3 = inbuf;
b4 = outbuf;
b9 = coefficients;
r0 = SECTIONS;
f8=dm(i3,m1); // read inbuf
r12=r12 xor r12, f2=dm(i0,m1), f4=pm(i8,m8);
lcntr=r0, do quads until lce;
f12=f2*f4, f8=f8+f12, f3=dm(i0,m1), f4=pm(i8,m8);
f12=f3*f4, f8=f8+f12, dm(i1,m1)=f3, f4=pm(i8,m8);
f12=f2*f4, f8=f8+f12, f2=dm(i0,m1), f4=pm(i8,m8);
quads:f12=f3*f4, f8=f8+f12, dm(i1,m1)=f8, f4=pm(i8,m8);
f8=f8+f12;
rts (db);
dm(i4,m1)=f8;
bit clr mode1 CBUFEN | PEYEN; // disable SIMD mode
_Cascaded_IIR_Filter_SIMD.end:
//--------------------------------------------
![y[n] = frac{1}{a_0} left ( b_0x[n] + b_1x[n-1] + b_2x[n-2] - a_1y[n-1] - a_2y[n-2]
ight )](http://upload.wikimedia.org/math/8/9/9/899682aeb49f324cb7c62272f1927738.png)
![y[n] = b_0x[n] + b_1x[n-1] + b_2x[n-2] - a_1y[n-1] - a_2y[n-2]](http://upload.wikimedia.org/math/3/5/b/35be336fc218dd9c7c086554a19a1d1f.png)


![y[n]=b_0 w[n]+b_1 w[n-1]+b_2 w[n-2],](http://upload.wikimedia.org/math/e/4/5/e45578623c01d6854eea37a32412d0f0.png)
![w[n]=x[n]-a_1 w[n-1]-a_2 w[n-2].](http://upload.wikimedia.org/math/4/3/8/4388a3c631cc110759e236f84b210b6f.png)