这个文章的目的是为了加强对这几个概念的理解与记忆。
怕自己不知道什么时候又忘了。
看自己写的东西总应该好理解记忆一些吧。
联合概率的乘法公式：
（当随机变量x，y独立，则
）
这太简单了是吧。。。。
联合概率公式变个形，得到条件概率公式为：
，
全概率公式：
，其中
可以这样理解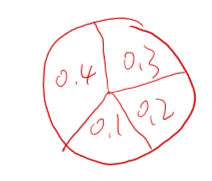
把一个圆看成x，其中被划分为好多种情况，对每一种情况的概率求和就是全概率（整个概率）。
（，则
可轻易推导出上式）
贝叶斯公式：
又名后验概率公式、逆概率公式。
后验概率
＝似然函数
*先验概率
/证据因子
。（是对上式最后一个等号的内容解释的）
举个例子。
假设我们根据“是否阴天”这个随机变量x（取值为“阴天”或“不阴天”）的观测样本数据,来判断是否会下雨（假设总共只有这两种类别下雨，不下雨）。我们根据经验来判断，比如根据历史数据估，阴天有70%会下雨，也就是说无须观测样本数据就知道下雨的先验概率（Prior Probability）较大。
接着，我们得到了的观测样本数据：“下雨”表现为阴天的 条件概率
（或者说这种“可能性”即似然（Likelihood））相比于”不下雨“表现为“阴天”的似然
较大。
所以经这次观测之后加强了我们的判断：下雨的后验概率（Posterior Probability）变得比先验概率更大，超过了之前的70%！
反之，则会减弱我们的判断，下雨的后验概率将小于70%。
因此，后验概率包含了先验信息以及观测样本数据提供的后验信息，对先验概率进行了修正，更接近真实情况。
此外，证据因子（Evidence，也被称为归一化常数）可仅看成一个权值因子，以保证各类别的后验概率总和为1从而满足概率条件。
如果我们的目标仅仅是要对所属类别做出一个判别：是“下雨”还是“不下雨”，则无须去计算后验概率的具体数值，只需计算哪个类别的后验概率更大即可。假设下雨和不下雨出现的先验概率相等
，则此时类别的判定完全取决于似然和的大小。因此，似然函数（Likelihood，“可能性”）的重要性不是它的具体取值，而是当参数（如类别参数）变化时，函数到底变小还是变大，以便反过来对参数进行估计求解（估计出是还是）。