OKR-Periods of Words【KMP最小前后缀】

OKR-Periods of Words

传送门：链接    来源：UPC 8180

题目描述

串是有限个小写字符的序列，特别的，一个空序列也可以是一个串。一个串P是串A的前缀，当且仅当存在串B，使得A=PB。如果P≠A并且P不是一个空串，那么我们说P是A的一个proper前缀。
定义Q是A的周期，当且仅当Q是A的一个proper前缀并且A是QQ的前缀（不一定要是proper前缀）。比如串abab和ababab都是串abababa的周期。串A的最大周期就是它最长的一个周期或者是一个空串（当A没有周期的时候），比如说，ababab的最大周期是abab。串abc的最大周期是空串。
给出一个串，求出它所有前缀的最大周期长度之和。

输入

第一行一个整数k，表示串的长度。
接下来一行表示给出的串。

输出

输出一个整数表示它所有前缀的最大周期长度之和。

样例输入

8
babababa

样例输出

24

提示

对于全部数据，1<k<106

思路:

kmp算法中的Next[i]代表的是最大前后缀，即位置i的前后缀最大的相同长度为Next[i]（若Next[0]=-1，长度即为Next[i]+1）。

这个题要求的是最小相同的前后缀（满足题目中周期的定义），可能不太好理解，看下图：（Next[0]=-1）

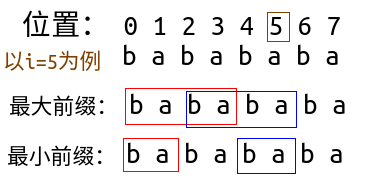
对应Next值：

求法：先正常求出Next数组，对每个Next[i]回溯到第一个不为-1的位置，并赋值给Next[i]。

例如当i=5时，Next[5]=Next[Next[5]]=1，其余同理。

AC代码：

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const LL MAX=1e6;
LL Next[MAX+5];
void getNext(string p,LL lp,LL Next[])
{
    LL k=-1;
    Next[0]=-1;
    for(LL i=1;i<lp;i++){
        while(k>-1&&p[k+1]!=p[i]) k=Next[k];
        if(p[k+1]==p[i]) k++;
        Next[i]=k;
    }
}
 
int main()
{
    LL lp;
    string p;
    cin>>lp>>p;
    getNext(p,lp,Next);
    for(LL i=0;i<lp;i++){
        if(Next[i]==-1) continue;
        else{
            while(Next[Next[i]]!=-1){
                Next[i]=Next[Next[i]];
            }
        }
    }
    LL sum=0;
    for(LL i=0;i<lp;i++){
        if(Next[i]!=-1)
            sum+=(i-Next[i]);
    }
    cout<<sum<<endl;
    return 0;
}