王小二切饼、马拦过河卒

1、王小二切饼

题目链接（点击）

Problem Description

王小二自夸刀工不错，有人放一张大的煎饼在砧板上，问他：“饼不许离开砧板，切n(1<=n<=100)刀最多能分成多少块？”

Input

输入切的刀数n。

Output

输出为切n刀最多切的饼的块数。

Sample Input

100

Sample Output

5051

思路：

求切n刀 饼最多的块的数目？

如图：

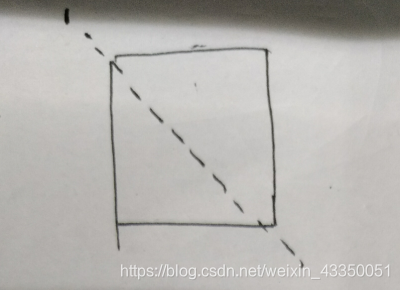
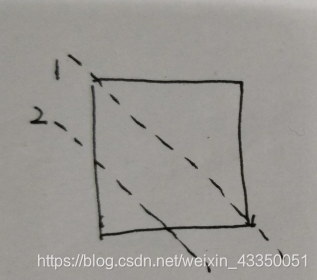
当分别切0、1刀最多分别1、2块，当切第三刀以及往后的时候： 

然后可以有下面两种切法：

(1) 、与第一次的线不相交：

(2) 、与第一次的线相交：

当与之前的线尽可能多的相交时，可以得到最多的块的数目。

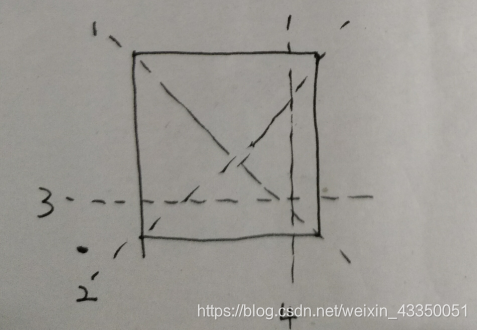
所以第三次以及后面的切法：（每次都与之前的线相交）

总结上面的快数目分别是：

1、2、4、7、11（分别对应0~4）

规律就很明显了：

          f(i)=f(i-1)+i

AC代码：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MAX=3e2;
int a[MAX+5];
int main()
{
    a[0]=1;
    for(int i=1;i<=105;i++){
        a[i]=a[i-1]+i;
    }
    int n;
    scanf("%d",&n);
    printf("%d
",a[n]);
    return 0;
}

2、马拦过河卒

Problem Description

棋盘上A点有一个过河卒，需要走到目标B点。卒行走的规则：可以向下、或者向右。同时在棋盘上C点有一个对方的马，该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。棋盘用坐标表示，A点（0，0）、B点（n，m）（n，m为不超过15的整数），同样马的位置坐标是需要给出的。现在要求你计算出卒从A点能够到达B点的路径的条数，假设马的位置是固定不动的，并不是卒走一步马走一步。

Input

一行四个数据，用空格分隔，分别表示B点的坐标和马的坐标。

Output

一个数据，表示所有的路径条数。

Sample Input

6 6 3 3

Sample Output

6

思路：

把这道题放在了递推里面，但我感觉是比较典型的dfs题目，因为之前做过一个迷宫的题目：传送门（解析）。

先打出x1*y1（根据题目中n点而定）的数组 ，然后再把马可以到达的位置用不同的数字标记。然后从左上到右下dfs，每次到达终点时cnt++，表示有一条新的可以到达终点的路径。

打出的表格如下（示例为题目样例输入）

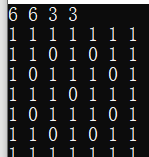
AC代码：

#include<bits/stdc++.h>
using namespace std;
int dir[2][2]={0,1,1,0};
int cnt;
int a[25][25];
int x1,x2,y11,y22;
void dfs(int x,int y)
{
    if(x==x1&&y==y11){
        cnt++;
        return;
    }
    for(int i=0;i<2;i++){
        x+=dir[i][0];  //借助方向数组dir改变x和y的值 实现走下一步
        y+=dir[i][1];
        if((a[x][y]==1)&&x>=0&&x<=x1&&y>=0&&y<=y11){
            a[x][y]=0;                  //x和y必须严格控制在矩阵内部
            dfs(x,y);
            a[x][y]=1;
        }
        x-=dir[i][0];  //实现返回
        y-=dir[i][1];
    }
}
int main()
{
    scanf("%d%d%d%d",&x1,&y11,&x2,&y22);
    for(int i=0;i<=x1;i++){
        for(int j=0;j<=y11;j++){
            a[i][j]=1;
        }
    }
    a[x2][y22]=0;
    a[x2-2][y22-1]=0;
    a[x2-2][y22+1]=0;
    a[x2-1][y22-2]=0;
    a[x2-1][y22+2]=0;
    a[x2+1][y22-2]=0;
    a[x2+1][y22-2]=0;
    a[x2+1][y22+2]=0;
    a[x2+2][y22-1]=0;
    a[x2+2][y22+1]=0;
    dfs(0,0);
    printf("%d
",cnt);
    return 0;
}