实践题目
2-3 蜜蜂路线 (20分)
问题描述
有一只经过训练的蜜蜂只能爬向右侧相邻的蜂房,不能反向爬行。请编程计算蜜蜂从蜂房a爬到蜂房b的可能路线数。 其中,蜂房的结构如下所示。
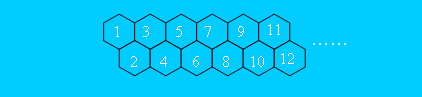
输入格式:
输入 m,n 的值, 0<m<n<30
输出格式:
一个整数,爬行有多少种路线
输入样例:
1 14
输出样例:
377算法描述
看图形,每到一个数,就有两条路可走,满足斐波那契数列的模型,因此这道题实际上还是用递归算法求解。不过这里应该注意的是,此时是逆向求解,要求f(1),得先一直递归直到能求f(12),再反过来求f(1)
#include <iostream> #define SIZE 15001 using namespace std; int f[SIZE] ; int main(){ int n, m, i; cin >> m >> n; f[m]=1; f[m+1]=1; for (i = m+2; i <= n; i++) f[i] = f[i-1] + f[i-2]; cout << f[n] << endl; return 0; }
算法时间及空间复杂度分析(要有分析过程)
时间复杂度:
复杂度实际上在与循环次数有关T(n) = 3 + 3 * (n - m + 1) =O(n)
空间复杂度:
因为每个变量空间复杂度为O(1),斐波那契数列的非递归算法空间复杂度为O(1)。
心得体会(对本次实践收获及疑惑进行总结)
其实这道题一开始我是完全读不懂题意,甚至那些样例我也看不懂,因为14,377都太大了,很难枚举找出关系,甚至后来上网查找有关这道题,我也还是搞不懂为什么这道题属于斐波那契数列,后来在博客上多看了其他人的做法学习,后来就慢慢理解了。这道题算是算法的入门级题吧,让我意识到一道奇奇怪怪的题,里面的做法都是来自算法的方法里,可能很难理解,但就是能用算法里的方法将这种奇怪的题化成书里那些经典的例题,像最近才做完的派这道题也是这样。