问题:
一副扑克牌。除去大小王后共52张牌,随机从中抽八张牌,问八张牌的和最有可能是多少?
分析:
这52张牌,事实上就是数字 1 2 3 。。。13, 每一个数字出现4次。随机抽出8个数,问组成的和最有可能是多少?
聪明的你可能想到了还有一个很相似的问题,2 sum: 问一个数组中是否存在两个数的和等于某个给定的值。
当然,这里就相似于 8 sum。
可是。题目却问的是,最有可能的结果是多少?
怎么分析呢?
最简单,但最有效的方法就是举个样例,就能理清思路了。
和最小的话就是 1 + 1 + 1 + 1 + 2 + 2 + 2 +2 = 12, 能够想象这个和12来说,出现的概率很之低。
相同,对于和 12*4 + 13*4= 100 来说,出现的概率相同很之低。
那么[12, 100] 中间的数呢? 能够想象,这些数有很多其它的数的组合,使得其和等于这个值, 因此概率更大。
大胆地猜想,(12 + 100)/2 = 56。 概率最大。越靠近这个和。出现的概率越大。
验证:
数学讲究严密性。
刚刚的猜想是建立的观測的基础之上的。
可是想必还是不能服众。
1. 还有一种简单的分析思路:
大家能够看看 1 2 ... 12 13 , 这13个数事实上是很对称的。
为什么这么说呢, 【1+13】= 【2+12】 = 【3+11】= 。
。。
。= 【6 + 8】
『高斯小的时候就发现了这个规律。。
』
上述的和都是 14, 也就是说,平均下来一个数就是7,因此7*8 = 56 的可能性最大。
当然,这样分析。不够严谨, 但有的时候。观察 + 猜想 = 成功
2. 咱们是学计算机呢,直接跑个程序验证不久 okay了。
最简单暴力的,就是枚举全部的情况。统计全部的和出现的次数。
当然,可能有人会说了。那不就是八重循环,吓死人啊....
能够採用 DFS, 就能避免写这么多个for 循环,代码例如以下:
//number[i]表示和为i的数目
int number[100];
void dfs(int cur, int count, int sum, int n)
{
if(count == 8){
++ number[sum];
return;
}
else if(cur > n){
return;
}
//5种选择
dfs(cur+1, count, sum, n);
dfs(cur+1, count+1, sum+cur, n);
dfs(cur+1, count+2, sum+2*cur, n);
dfs(cur+1, count+3, sum+3*cur, n);
dfs(cur+1, count+4, sum+4*cur, n);
}
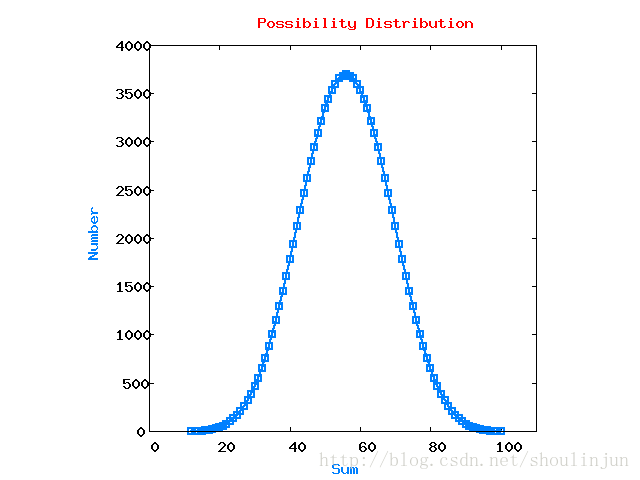
实验例如以下:gnuplot 画的这线图,支持开源。。