加工零件(Dijkstra)

题目描述

凯凯的工厂正在有条不紊地生产一种神奇的零件，神奇的零件的生产过程自然也很神奇。工厂里有n位工人，工人们从1~n编号。某些工人之间存在双向的零件传送带。保证每两名工人之间最多只存在一条传送带。
如果x号工人想生产一个被加工到第L(L>1)阶段的零件，则所有与x号工人有传送带直接相连的工人，都需要生产一个被加工到第L-1阶段的零件（但x号工人自己无需生产第L-1阶段的零件）。
如果x号工人想生产一个被加工到第1阶段的零件，则所有与x号工人有传送带直接相连的工人，都需要为x号工人提供一个原材料。
轩轩是1号工人。现在给出q张工单，第i张工单表示编号为ai的工人想生产一个第Li阶段的零件。轩轩想知道对于每张工单，他是否需要给别人提供原材料。他知道聪明的你一定可以帮他计算出来！

输入

第一行三个正整数n,m和q，分别表示工人的数目、传送带的数目和工单的数目。
接下来m行，每行两个正整数u和v，表示编号为u和v的工人之间存在一条零件传输带。保证u!=v。
接下来q行，每行两个正整数a和L，表示编号为a的工人想生产一个第L阶段的零件。

输出

共q行，每行一个字符串Yes或者No。如果按照第i张工单生产，需要编号为1的轩轩提供原材料，则在第i行输出Yes；否则在第i行输出No。注意输出不含引号。

样例输入

3 2 6

1 2

2 3

1 1

2 1

3 1

1 2

2 2

3 2

样例输出

Yes

提示

样例输入2：

5 5 5

1 2

2 3

3 4

4 5

1 5

1 1

1 2

1 3

1 4

1 5

样例输出2：

Yes

【输入输出样例 1 说明】

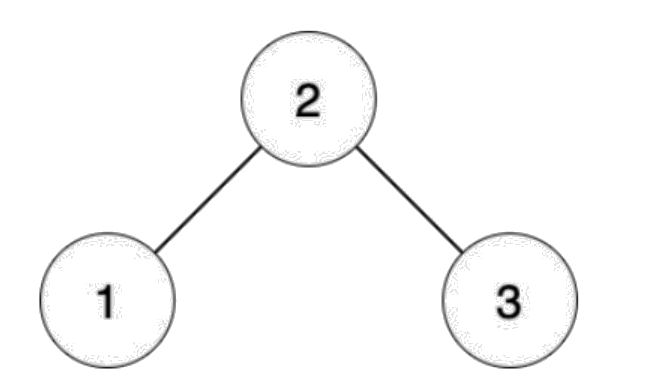
编号为 1 的工人想生产第 1 阶段的零件，需要编号为 2 的工人提供原材料。

编号为 2 的工人想生产第 1 阶段的零件，需要编号为 1 和 3 的工人提供原材料。

编号为 3 的工人想生产第 1 阶段的零件，需要编号为 2 的工人提供原材料。

编号为 1 的工人想生产第 2 阶段的零件，需要编号为 2 的工人生产第 1 阶段的零件，需要编号为 1 和 3 的工人提供原材料。

编号为 2 的工人想生产第 2 阶段的零件，需要编号为 1 和 3 的工人生产第 1 阶段的零件，他/她们都需要编号为 2 的工人提供原材料。

编号为 3 的工人想生产第 2 阶段的零件，需要编号为 2 的工人生产第 1 阶段的零件，需要编号为 1 和 3 的工人提供原材料。

【输入输出样例 2 说明】

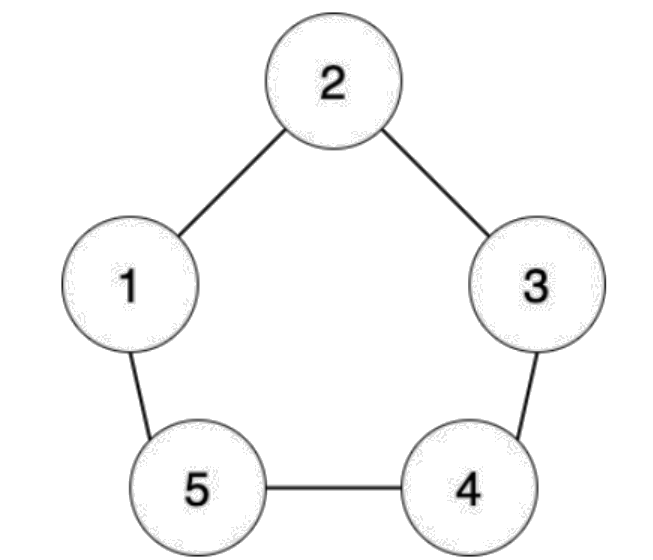
编号为 1 的工人想生产第 1 阶段的零件，需要编号为 2 和 5 的工人提供原材料。

编号为 1 的工人想生产第 2 阶段的零件，需要编号为 2 和 5 的工人生产第 1 阶段的零件，需要编号为

编号为 1 的工人想生产第 3 阶段的零件，需要编号为 2 和 5 的工人生产第 2 阶段的零件，需要编号为

编号为 1 的工人想生产第 4 阶段的零件，需要编号为 2 和 5 的工人生产第 3 阶段的零件，需要编号为

编号为 1 的工人想生产第 5 阶段的零件，需要编号为 2 和 5 的工人生产第 4 阶段的零件，需要编号为

数据规模与约定

共 20 个测试点。

测试点 1~4，

测试点 5~8，

测试点 9~12，

测试点 13~16， $1≤n,m,L≤1000，1≤q≤10^5。$

测试点 17~20， $1≤n,m,q≤105，1≤L≤10^9。$

题意：

　　其实这道题相当于给出了边权都为1的一张无向图，求1到x之间有没有一条长为L的路径，如果有1号就需要生产原料。

　　其实能想到这里，这道题差不多就解决了。

　　首先，如果1到x之间有一条路径是a，那么肯定有一条路径长度为a+2。为什么呢？一条路径多走几遍就好了啊啊啊。但是a+1的路径不一定能达到。

　　所以我们只需要求一遍单源最短奇偶路，求出每个点到1的最短且长度为分别为奇数和偶数的两条路径，如果L是奇数并且小于x的奇数最短路，那么就输出“Yes”；反之输出“No”，偶数亦然。

代码：

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<cstring>
 4 #include<queue>
 5 #define N 1000005
 6 using namespace std;
 7 int n,m,c,head[N],cnt,dis[N][2];
 8 bool vis[N][2];
 9 struct node{
10     int u,v;
11     bool operator<(const node &a)const{ return a.v<v; }
12     node(const int &u,const int &v):u(u),v(v){}
13 };
14 priority_queue<node> q;
15 struct Edge{ int to,next; }e[N];
16 void add(int u,int v)
17 {
18     e[++cnt].to=v;
19     e[cnt].next=head[u];
20     head[u]=cnt; 
21 }
22 void dijkstra()
23 {
24     memset(dis,0x3f,sizeof(dis));
25     q.push((node){1,0}),dis[1][0] = 0;
26     while(!q.empty())
27     {
28         int x=q.top().u;  q.pop();
29         for(int i=head[x];i;i=e[i].next)
30         {
31             int y=e[i].to;
32             if(dis[y][0]>dis[x][1]+1)
33             {
34                 dis[y][0]=dis[x][1]+1;
35                 if(!vis[y][0])
36                 {
37                     vis[y][0]=1;
38                     q.push(node(y,dis[y][0]));
39                 }
40             }
41             if(dis[y][1]>dis[x][0]+1)
42             {
43                 dis[y][1]=dis[x][0]+1;
44                 if(!vis[y][1])
45                 {
46                     vis[y][1]=1;
47                     q.push(node(y,dis[y][1]));
48                 }
49             }
50         }
51     }
52 }
53 int main(){
54     scanf("%d %d %d",&n,&m,&c);
55     for(int i=1;i<=m;i++)
56     {
57         int u,v;
58         scanf("%d %d",&u,&v);
59         add(u,v),add(v,u);
60     }
61     if(!head[1])
62     {
63         for(int i=1;i<=c;i++)  printf("No
");
64         return 0;
65     }
66     dijkstra();
67     while(c--)
68     {
69         int x,L;
70         scanf("%d %d",&x,&L);
71         if(dis[x][L%2]<=L)  printf("Yes
");
72         else  printf("No
");
73     }
74 return 0;
75 }