如何用整数规划求解NP完全问题
一、NP完全问题
NP完全问题是一类具有非常高难度的组合最优化问题, 所有NP完全问题都是NP难问题。虽然P问题是比较容易的问题, NP问题却不一定是困难问题,必须看见NP完全或者NP难这样的字才能说这个问题求解起来很困难。
经常听砖家说,NP完全/NP难问题不能用整数规划求解。实际情况怎样?实事证明砖家的话只能信一半:)。这里咱就看看用整数规划求解一个NP完全问题行也不行。
这里有一个货真价实的整数规划问题——划分问题(The partition problem)。问题是:给定一个大小不等的整数集合,问是否可以把这些整数划分成两个集合,任何一个整数或者在集合S1中或者在S2中,但不能同时在两个集合中;对任意给的一个整数集合,请设计算法,解决是否存在一个划分,使得S1种整数之和恰好等于S2集合的整数之和。
二、建立整数规划模型
对每个整数定义一个0-1变量xi, xi=1 表示第i个整数位于集合S1中, xi=0表示第i个整数位于S2中。用s1表示第一集合的整数之和,用s2表示第二个集合里的整数之和。即:
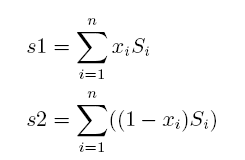
设d是s1和s2之间差的绝对值。于是:
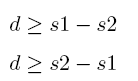
我们只要极小化d就可以了,即:
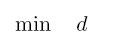
完整模型:
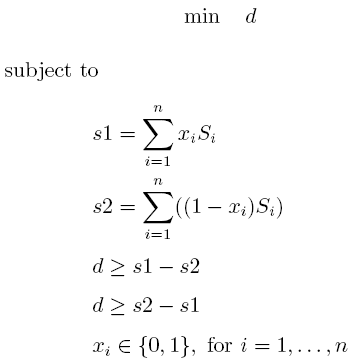
三、上面的模型的文本表达
上面的模型不只是用来摆摆看的,还可以真的被求解哈。我们需要把模型写成文本格式(Leapms建模语言格式),让计算机理解。目标函数就写成
min d
加上其余约束部分(注意西格玛符合的写法)
subject to s1=sum{i=1,...,n}x[i]S[i] s2=sum{i=1,...,n}((1-x[i])S[i]) d>=s1-s2 d>=s2-s1
加上符号说明(符号必须说明,不然计算机不知道哪些是常数,哪些是变量)
where n is an integer S is a set s1,s2,d are variables of number x[i] is a variable of binary|i=1,...,n
加上数据(注意整数个数是从集合S上自己数出来的)
data_relation n=_$(S) data S={11,47,159,137,85,47,142,35,119,61,88,175,13,96,-11,176,126,15,98,46,163}
四、求解
把如下完整模型贴到记事本上,保存为 partition.leap文件。(注意如果是partition.txt不行啊)。
min d subject to s1=sum{i=1,...,n}x[i]S[i] s2=sum{i=1,...,n}((1-x[i])S[i]) d>=s1-s2 d>=s2-s1 where n is an integer S is a set s1,s2,d are variables of number x[i] is a variable of binary|i=1,...,n data_relation n=_$(S) data S={11,47,159,137,85,47,142,35,119,61,88,175,13,96,-11,176,126,15,98,46,163}
启动leapms,依次打入load, partion, mip命令,即可得到解
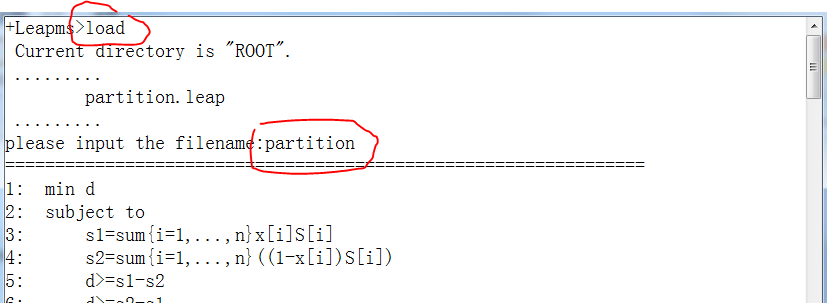

如果需要用cplex求解,打入cplex命令即可。如果你的leapms版本不支持直接cplex调用,使用savemps命令把模型保存成mps格式而后用cplex求解(见 https://www.cnblogs.com/leapms/p/11843946.html)。
五、结果分析
上面的结果d=0, s1=s2=914。显然对给出的数据来说,有划分。
整数规划成功求解了一个NP完全问题。