zoukankan      html  css  js  c++  java

  • 堆排序

    堆排序是非常快的一种排序方法。其时间复杂度为O(nlogn)，和快速排序不相上下。

    什么是堆

    我们在介绍堆排序之前，当然需要知道什么是堆。堆是一种数据结构，相当于二叉树一样。但是它是使用数组存放的。存放的方法是：从左到右，从上到下地将节点依此放入数组中：

     

     像图中的二叉树，首先从顶端开始将34放入数组中。然后来到第二层，将28，16放入数组中。然后来到第三层，将15，14，9，1放入数组中...以此类推。如果你是将数组变为二叉树的话就是一个相反的过程：先将34置为树根，然后从左到右，从上到下的依次添加节点。注意这里我说的是变成二叉树而不是变成堆，因为很有可能这个数组对应的二叉树不满足堆的性质。
     
    堆的性质：
    堆不仅仅是二叉树，它还有自己的性质：
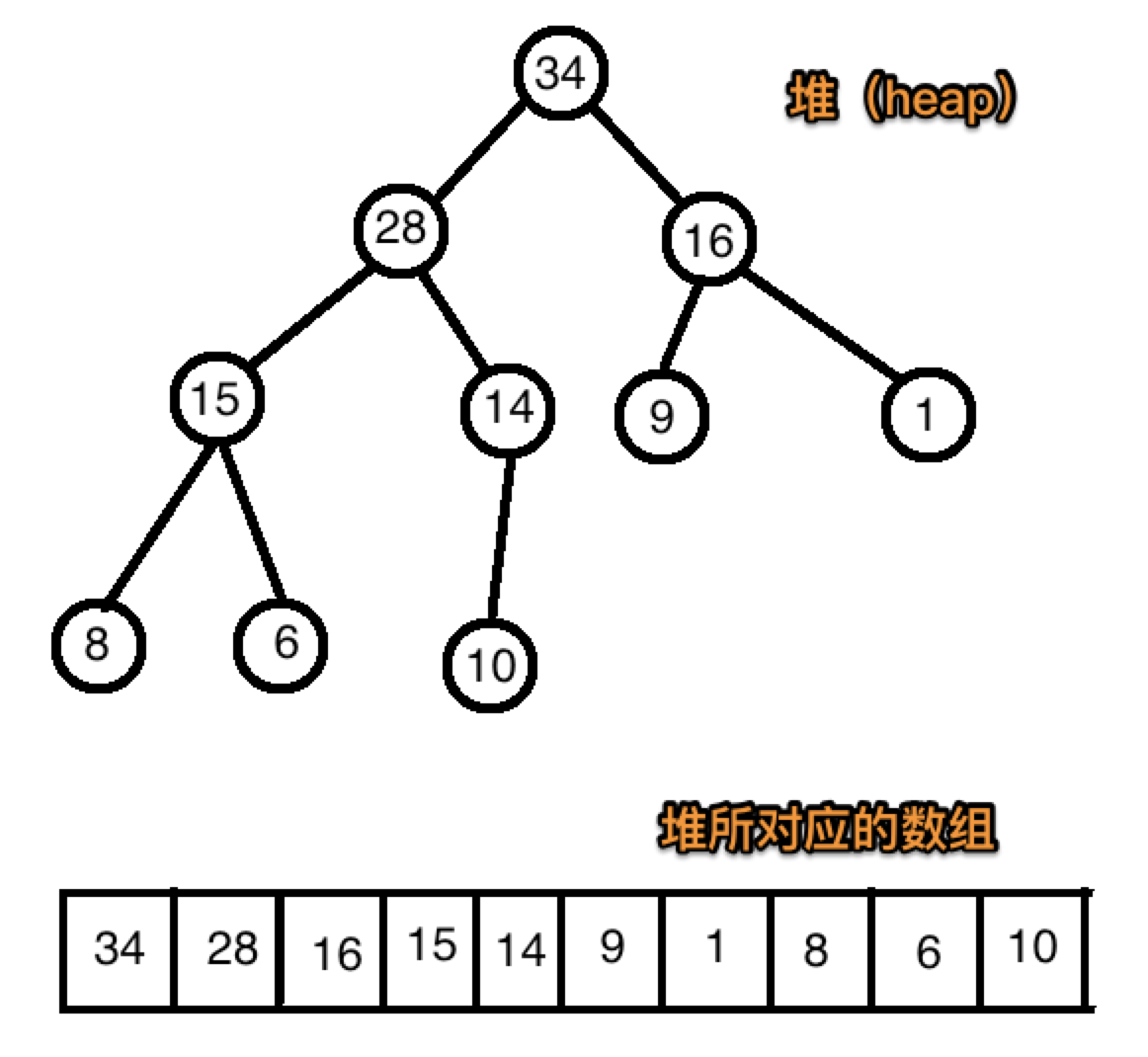
    • 任何一个节点的数值一定比两个子节点都大

    有这个性质的堆称为最大堆，如果反过来：

    • 任何一个节点的数值一定比其子节点都小

    那么就是最小堆。

    最大堆最后排序出来的元素是升序的。最小堆对应降序排列。

    堆还有一个隐含的性质：

    • 每一个堆都是完全二叉树

    这个性质很容易被发现：由于我们从数组生成二叉树时总是自左向右，自上而下的，所以最后的结果一定是最下层的最右边空缺，所以一定会生成完全二叉树。

     堆的拓展性质：

    接下来通过性质我们还可以推导出一些十分有用的拓展性质，我们需要使用这些性质来进行堆排序：

    1. 对于有n个元素的堆来说，其二叉树高度为floor(logn)。（其中floor为向下取整）

      这个性质的证明还是比较简单的。可以看出层数h和当前层的节点数n的关系是n=2^(h-1)。这样使用求和公式，最后考虑最下一层不全部排满的情况就可以推导出这个公式了。

    2. 对于一个有n个元素的堆来说，第floor(n/2)+1个元素为第一个叶子节点，floor(n/2)+2为第二个叶子结点...依此类推。
    3. 对于第n个父节点来说，其左节点是第2*n个节点，右节点是第2*n+1个节点

    维护堆的性质 

    对于一个数据结构，我们需要做到在插入，删除元素的时候不改变数据结构的性质。这里我们以最大堆为例来说明如何维护堆的性质：

    最大堆的性质是：

    　　任何一个父节点都比两个子节点的数值要大。

    我们需要在更改堆的时候让堆不违反这个性质。我们这里使用一个函数来维护堆的性质。这个函数将在每次打乱堆的时候使堆自动变成符合性质的结构：

     1 LEFT(n)
 2     return n*2
 3 
 4 RIGHT(n)
 5     return n*2+1
 6 
 7 MAX_HEAP(heap,i)
 8     left=LEFT(i)
 9     right=RIGHT(i)
10     if(left<=length && heap[left]>heap[I])
11         max=left
12     Else 
13         max=I
14     If(right<=length && heap[right]>heap[max])
15         max =right
16     if(max!=i)
17         Exchange heap[I] and heap[max]
18         MAX_HEAP(heap,max)

    首先根据拓展性质3，LEFT()和RIGHT()函数用于获得节点n的左右节点的下标。

    接下来MAX_HEAP用于维护堆的性质： 

    　　第8，9行获得节点i的左右子节点。

    　　第10，14行比较这个节点和其子节点的大小，并且将三者中最大的节点下标记录在max中。

    　　第16行判断最大的节点是不是原本的父节点i。如果是的话就停止维护堆的性质。否则再次递归调用MAX_HEAP()函数向下维护堆的性质。

    对于递归，我们知道总是有一个基础步骤和一个递归步骤：

    基础步骤：对于节点i，找出i，i的子节点中最大的节点下标，放入max中。

    递归步骤：如果max!=i，则交换heap[max]和heap[i]的值，并且调用MAX_HEAP(heap,max)

    这就是MAX_HEAP函数的递归描述。

    具体的C++代码如下：

    堆的类结构：

    template <typename T>
class Heap{
public:
    Heap():heap(nullptr),len(0){}
    Heap(T* arr,int l);
    vector<T> GetSortedVector();
    void OutPut();
    ~Heap();
private:
    T GetLeft(int i);
    T GetRight(int i);
    void Max_Heap(int i);
    void Max_Heap_for_Sort(T* arr,int i,int length);
    void CreateHeap();
    T* heap;
    int len;
};
    类结构

    维护堆性质的代码：

    template <typename T>
T Heap<T>::GetLeft(int i){
    return heap[i<<1];
}

template <typename T>
T Heap<T>::GetRight(int i){
    if((i<<1)+1 > len)
        return INT_MIN;
    return heap[(i<<1)+1];
}

template <typename T>
void Heap<T>::Max_Heap(int i){
    int max;
    T l=GetLeft(i),r=GetRight(i);
    if((i<<1)<=len && l>heap[i])
        max=i<<1;
    else
        max=i;
    if((i<<1)+1<=len && r>heap[max])
        max=(i<<1)+1;
    if(max!=i){
        int temp=heap[max];
        heap[max]=heap[i];
        heap[i]=temp;
        Max_Heap(max);
    }
}
    维护性质 

     构建堆 

    由于是排序算法，所以首先一定会给出一些数，这些数常常放在数组中，像是这样： 

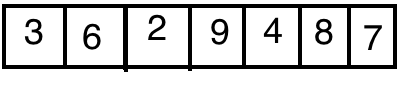
    我们就将这个数组当作一个二叉树，那么根据上面说的规则，采用自左向右，自上而下的方式构建二叉树： 

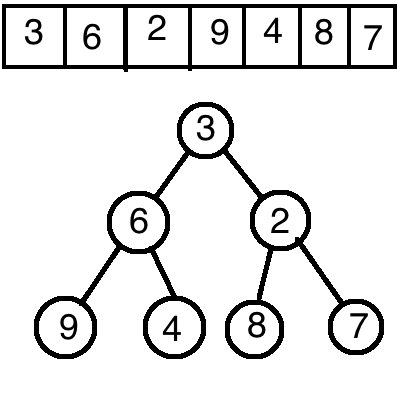
    现在这个还只是二叉树。要将这棵树变成堆，需要满足堆的性质。这样的话维护堆性质的函数就派上用场了。我们自底向上的对，每个父节点使用MAX_HEAP函数来将二叉树变成堆（也就是说最下一层不使用）：

    CEATE_HEAP(heap)
    For i=floor(length/2) downto 1
        MAX_HEAP(heap,i)

    其中第二行的for循环用于从下到上的使用MAX_HEAP函数。这里floor(lengtth/2)的条件是根据拓展性质3得出的。

    对应的C++代码如下： 

    template <typename T>
void Heap<T>::CreateHeap(){
    for(int i=floor(len/2);i>=1;i--)
        Max_Heap(i);
}
    构建堆

     对于上面的树，变成堆堆过程如下： 

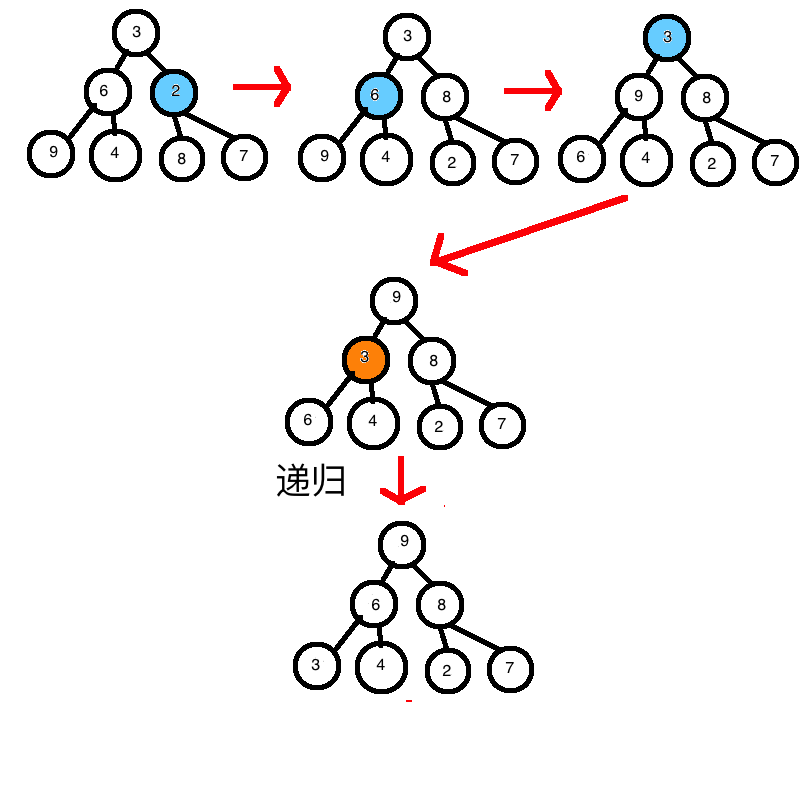
    其中蓝色是for循环里MAX_HEAP()执行到的节点。橙色的是MAX_HEAP()递归递归到的节点。

    可能会有些人说，为什么要自底向上创建，我自顶向下创建不行吗？下面我们来看看自顶向下的创建过程（只需要将for循环里改成i=1 to floor(length/2)即可）

     

    可以看出最后的结果并不正确。

     

    堆排序 

    终于到了我们最后这一章的核心，堆排序了。其实前面说的都是如何创建堆这个数据结构。接下来通过这个数据结构来进行排序。

    堆排序的思想如下：

    根据最大堆的性质（你要是使用的最小堆就看最小堆的性质），父节点总是比子节点大。这样的话堆的根节点一定是整个堆里面最大的节点。我们可以把这个节点和最右下角的节点互换：

      

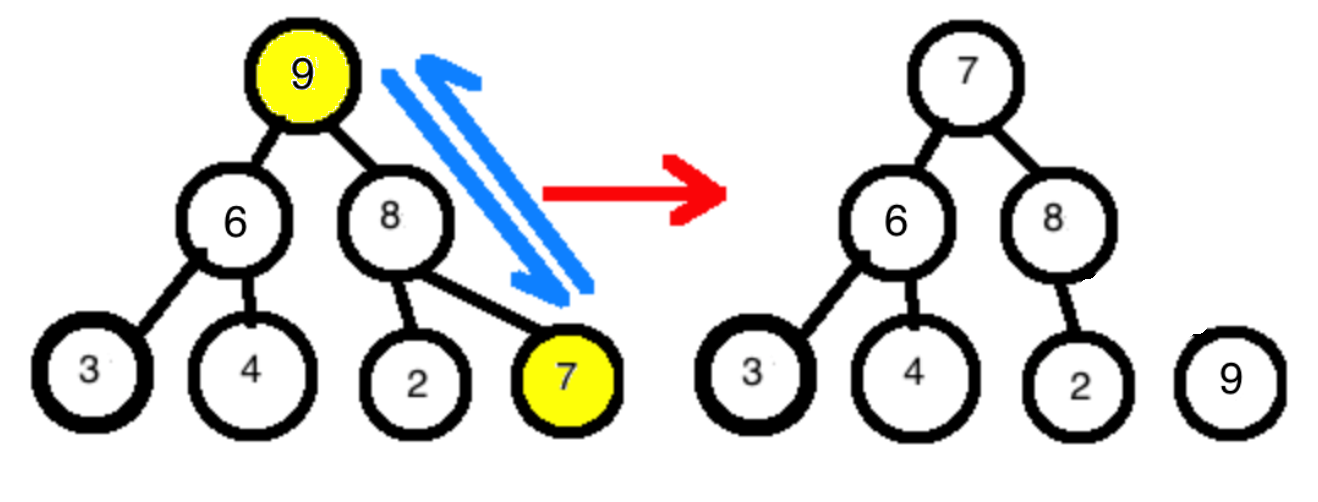
    为什么要和最右下角的节点互换呢？不要忘记这颗树是通过数组存储的哦。我们把最大元素和最右下角的元素互换，其实就是将最大元素和数组最后一个元素互换哦： 

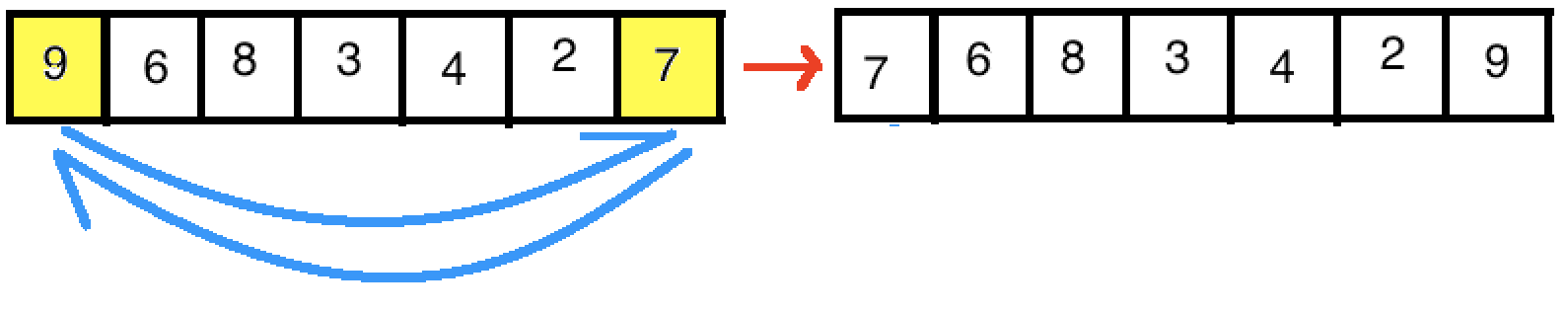
    这个时候右下角的节点就已经不属于堆了。

    但是这样做的话又破坏了堆的性质（这里7小于8了），所以我们需要再次维护堆的性质，对根节点调用MAX_HEAP即可：

     

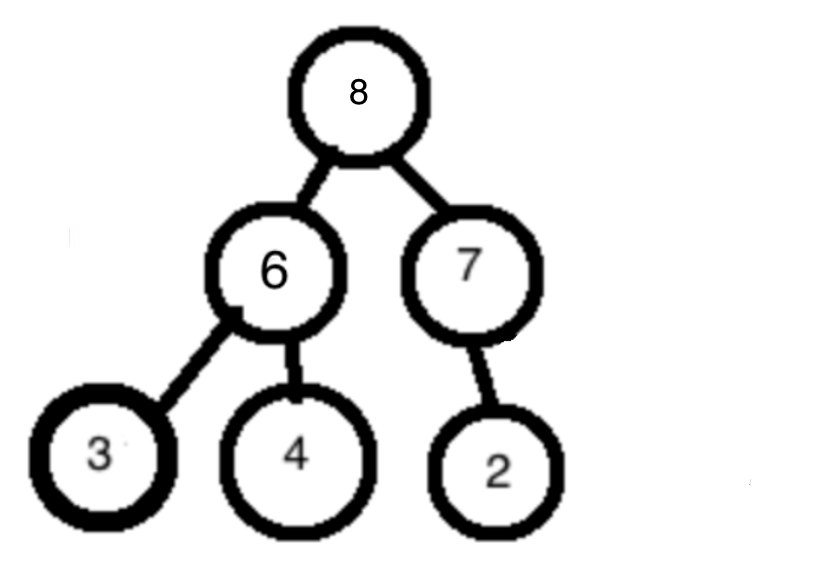
    由于原本最大的节点已经放到数组的最后一位了，现在堆里面的节点全部都小于数组最右边的节点。通过维护堆的性质再将堆中最大节点放到根节点处。这个时候根节点是整个排序数组中第二大节点。然后将根节点放到倒数第二个节点处就完成了一次排序。

    然后重复地将根节点和右下方的节点互换，再对根节点使用MAX_HEAP。直到堆里面没有节点了，排序就完成了。

    伪代码如下：

    HEAPSORT(heap)
    For i=length downto 2
        Exchange heap[i] and heap[1]
        Length--
        MAX_HEAP(heap,1)

    C++代码如下：

    template <typename T>
void Heap<T>::Max_Heap_for_Sort(T* arr,int i,int length){
    int max,r,l;
    l=i<<1;
    r=(i<<1)+1;
    if(l<=length && arr[l]>arr[i])
        max=l;
    else
        max=i;
    if(r<=length && arr[r]>arr[max])
        max=r;
    if(max!=i){
        int temp=arr[i];
        arr[i]=arr[max];
        arr[max]=temp;
        //length--;
        Max_Heap_for_Sort(arr, max, length);
    }
    for(int i=1;i<=len;i++)
        cout<<arr[i]<<",";
    cout<<endl;
}
    堆排序

    最后数组就被排序成功了。

    下面是C++的全部实现代码：

    #ifndef Heap_hpp
#define Heap_hpp

#include <iostream>
#include <cmath>
#include <vector>
using namespace std;

template <typename T>
class Heap{
public:
    Heap():heap(nullptr),len(0){}
    Heap(T* arr,int l);
    vector<T> GetSortedVector();
    void OutPut();
    ~Heap();
private:
    T GetLeft(int i);
    T GetRight(int i);
    T GetParent(int i);
    void Max_Heap(int i);
    void Max_Heap_for_Sort(T* arr,int i,int length);
    void CreateHeap();
    T* heap;
    int len;
};

template <typename T>
Heap<T>::Heap(T* arr,int l):len(l){
    heap=new T[l+1];
    for(int i=0;i<l;i++)
        heap[i+1]=arr[i];
    CreateHeap();
}

template <typename T>
T Heap<T>::GetLeft(int i){
    return heap[i<<1];
}

template <typename T>
T Heap<T>::GetRight(int i){
    if((i<<1)+1 > len)
        return INT_MIN;
    return heap[(i<<1)+1];
}

template <typename T>
T Heap<T>::GetParent(int i){
    return heap[i>>1];
}

template <typename T>
void Heap<T>::Max_Heap(int i){
    int max;
    T l=GetLeft(i),r=GetRight(i);
    if((i<<1)<=len && l>heap[i])
        max=i<<1;
    else
        max=i;
    if((i<<1)+1<=len && r>heap[max])
        max=(i<<1)+1;
    if(max!=i){
        int temp=heap[max];
        heap[max]=heap[i];
        heap[i]=temp;
        Max_Heap(max);
    }
}


template <typename T>
void Heap<T>::Max_Heap_for_Sort(T* arr,int i,int length){
    int max,r,l;
    l=i<<1;
    r=(i<<1)+1;
    if(l<=length && arr[l]>arr[i])
        max=l;
    else
        max=i;
    if(r<=length && arr[r]>arr[max])
        max=r;
    if(max!=i){
        int temp=arr[i];
        arr[i]=arr[max];
        arr[max]=temp;
        //length--;
        Max_Heap_for_Sort(arr, max, length);
    }
    for(int i=1;i<=len;i++)
        cout<<arr[i]<<",";
    cout<<endl;
}

template <typename T>
vector<T> Heap<T>::GetSortedVector(){
    vector<T> v;
    T temp[len+1];
    int length=len;
    for(int i=0;i<=len;i++)
        temp[i]=heap[i];
    for(int i=len;i>=2;i--){
        v.push_back(temp[1]);
        temp[1]=temp[i];
        Max_Heap_for_Sort(temp, 1, --length);
    }
    return v;
}

template <typename T>
void Heap<T>::OutPut(){
    for(int i=1;i<=len;i++)
        cout<<heap[i]<<",";
    cout<<endl;
}

template <typename T>
Heap<T>::~Heap(){
    if(heap!=nullptr)
        delete[] heap;
}
#endif
    全代码
  • 相关阅读:
    wrk压测工具使用
    Mac 抓包工具wireshark使用
    hadoop无法停止
    非root用户如何使用docker命令
    too many open files
    kafka性能测试1.0.0
    命令查看linux主机配置
    ELK(Logstash＋Elasticsearch＋Kibana)的原理和详细搭建
    分布式session实现
    NUC972裸机调试步骤
  • 原文地址：https://www.cnblogs.com/learn-program/p/9613042.html
Copyright © 2011-2022 走看看