点分治学习笔记
前言
今天(19.7.11)B组比赛T2是点分治的题。震惊之余赶紧学一学。
正文
用途
点分治主要用来解决统计树上路径的问题。常见的有:
- 路径和等于或小于等于k的点对(路径条数)。
- 路径和为某个数的倍数。
- 路径和为k且路径的边数最少。
- 路径和mod M后为某个值。
- 路径上经过不允许点的个数不超过某个值,且路径和最大。
时间复杂度通常为O((nlogn))或O((nlog^2n)),视solve函数的具体打法而定
前置知识
树的重心
定义
一颗无根树中最大子树大小最小的节点。
性质
设整棵树的大小为size,最大子树的大小不超过size/2
证明:反证法
算法流程
- 计算经过当前关键点(就是当前子树的重心)的路径,把路径两两匹配统计答案
- 枚举重心的每一个儿子
- 将答案减去经过只同一个儿子的路径(去重)
- 找儿子子树的重心
- 递归分治儿子
为什么3.要去重呢?
以下内容来自[点分治详细解析][https://blog.csdn.net/qq_39553725/article/details/77542223]
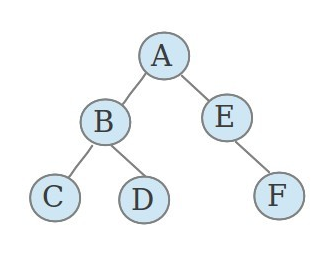
当我们以A为关键点计算答案时,我们会统计如下几条路径
A—>A
A—>B
A—>B—>C
A—>B—>D
A—>E
A—>E—>F (按照先序遍历顺序罗列)
那么我们在合并答案是会将上述6条路径两两进行合并。
这是注意到:
合并A—>B—>C 和 A—>B—>D 肯定是不合法的!!
因为这并不是一条树上(简单)路径,出现了重边,我们要想办法把这种情况处理掉。
处理方法很简单,减去每个子树的单独贡献。
例如对于以B为根的子树,就会减去:
B—>B
B—>C
B—>D
这三条路径组合的贡献
例题
树中点对距离
给出一棵带边权的树,问有多少对点的距离<=Len
裸题嘛
把板子套一下就好了
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int n,len,i,j,mi,root,Size,ans;
int x,y,z;
int l[20005][2],next[20005],last[10005],tot;
int size[20005];
int dis[20005];
int bz[10005];
void insert(int x,int y,int z)
{
tot++;
l[tot][0]=y;l[tot][1]=z;
next[tot]=last[x];
last[x]=tot;
}
void getroot(int x,int fa)
{
int mason=0;
size[x]=1;
for (int i=last[x];i>=1;i=next[i])
{
if ((l[i][0]!=fa)&&(bz[l[i][0]]==0))//记得判断l[i][0]是否曾经分治过
{
getroot(l[i][0],x);
size[x]+=size[l[i][0]];
mason=max(mason,size[l[i][0]]);
}
}
mason=max(mason,Size-size[x]);
if (mi>mason)
{
mi=mason;
root=x;
}
}
void getdis(int x,int fa,int len)
{
dis[++dis[0]]=len;
for (int i=last[x];i>=1;i=next[i])
{
if ((l[i][0]!=fa)&&(bz[l[i][0]]==0))
{
getdis(l[i][0],x,len+l[i][1]);
}
}
}
int solve(int x,int d)
{
dis[0]=0;
getdis(x,0,d);
sort(dis+1,dis+1+dis[0]);
int bz=0,s=0;
for (int i=dis[0];i>=1;i--)
{
while ((bz<=i)&&(dis[bz+1]+dis[i]<=len))
bz++;
while (bz>=i)
bz--;
s=s+bz;
}
return s;
}
void Divide(int x,int SSize)
{
bz[x]=1;//记得标记
ans+=solve(x,0);
for (int i=last[x];i>=1;i=next[i])
{
int y=l[i][0];
if (bz[y]) continue;//记得判断是否分治过
ans-=solve(y,l[i][1]);
if (size[y]<size[x]) Size=size[y];
else Size=SSize-size[x];//重点,计算以y为根子树的大小
mi=1000000;//记得赋初值
getroot(y,x);
Divide(root,Size);
}
}
int main()
{
freopen("read.in","r",stdin);
scanf("%d%d",&n,&len);
for (i=1;i<=n-1;i++)
{
scanf("%d%d%d",&x,&y,&z);
insert(x,y,z);
insert(y,x,z);
}
memset(bz,0,sizeof(bz));
mi=1000000;Size=n;
getroot(1,0);
Divide(root,n);
printf("%d",ans);
}