8.13总结

今天的比赛真是爽死了
三道计数题
得分
30+20+10
Rank9
惨不忍睹
T1
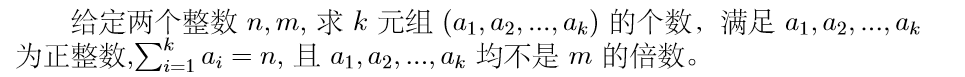
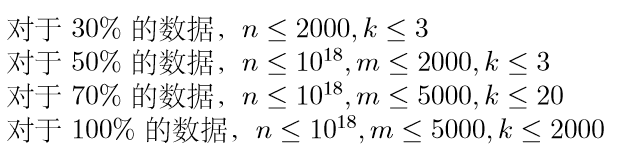
正解

枚举A,枚举有几个元素值大于m-1来容斥。偶加奇减。
由于要固定几个元素大于m-1,所以从A里面减掉i*(m-1)来钦定i个元素大于m-1。剩下的A随便分,再随便从k个里面选i个加上m-1来使它们大于m-1。
T2

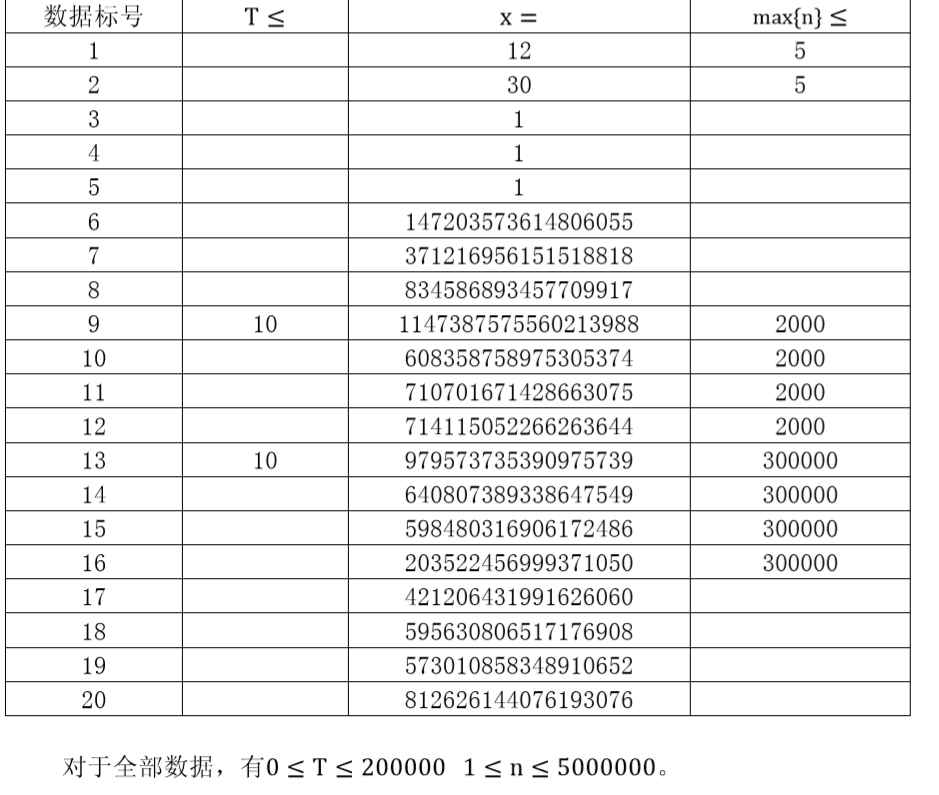
正解
全部x都给出了,肯定有玄机。观察发现全部x的质因子次数最大为2。
每个质因子可以分开考虑。只要每个质因子在每一行每一列的乘积合法,总的矩阵也是合法的。思考发现,答案可以分为三个部分,即:符号的方案数*一次质因子的方案数*二次质因子的方案数。
符号的方案数即为(2^{(n-1)^2})
一次质因子的方案数即为(n!)
二次质因子的方案数有点难算。设f[i]表示i*i的矩形最后一列放了两个1的方案数,g[i]表示i*i的矩形最后一列放了一个二的方案数。
(g[i]=(f[i-1]+g[i-1])*i)
(f[i]=C_i^2*(2f[i-1]+g[i-1]))
这两条式子跟别人研究了很久也没搞懂。
T3


正解
我们发现,一个合法的序列一定对应一个前缀max序列。

所以我们只要统计出有多少中合法的前缀max序列就能直接得到答案了
关键是怎么合法的前缀max序列要满足哪些条件。

对与y<x的情况与把y和x交换的情况是等价的。因为可以把那个排列的下标和权值交换,仍然是一个合法的序列。

问题转化为求在一个平面直角坐标系上经过点(x,y)但不经过直线y=x-1的(1,1)到(n,n)的路径数量,直接用翻折法求即可。