问题
编写用二分法求![]() 在区间[1,1.5]内的一个根的程序,收敛误差不超过
在区间[1,1.5]内的一个根的程序,收敛误差不超过![]() 。在同一图形上分别画出
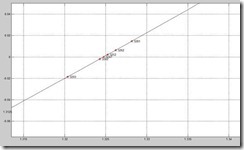
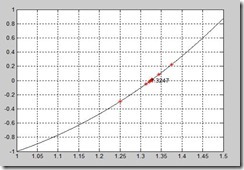
。在同一图形上分别画出![]() 的图形及每一中点对应的函数值,以观察收敛过程。
的图形及每一中点对应的函数值,以观察收敛过程。
原理
设![]() 在区间[a,b]上连续,且
在区间[a,b]上连续,且![]() ,根据连续函数性质可知
,根据连续函数性质可知![]() 在[a,b]内一定有根,并称[a,b]为方程
在[a,b]内一定有根,并称[a,b]为方程![]() 的有根区间。
的有根区间。
其中每个区间是前一个区间的一半,二分![]() 次以后得有根区间[
次以后得有根区间[![]() ],其长度是
],其长度是
由此,如果二分过程无限地进行下去(![]() ),则有限区间根必定缩为一点,该点就是所求的根。在此过程我们一般都确定误差范围出结果。
),则有限区间根必定缩为一点,该点就是所求的根。在此过程我们一般都确定误差范围出结果。
在此题目中
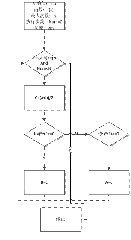
程序框图
结果比较
| 0 | 1 | 1.5 | 1.25 | - |
| 1 | 1.2500 | 1.5 | 1.3750 | + |
| 2 | 1.2500 | 1.3750 | 1.3125 | - |
| 3 | 1.3125 | 1.3750 | 1.3438 | + |
| 4 | 1.3125 | 1.3438 | 1.3281 | + |
| 5 | 1.3125 | 1.3281 | 1.3203 | - |
| 6 | 1.3203 | 1.3281 | 1.3242 | - |
| 7 | 1.3242 | 1.3281 | 1.3262 | + |
| 8 | 1.3242 | 1.3262 | 1.3252 | + |
| 9 | 1.3242 | 1.3252 | 1.3247 | - |
结论
附件:程序
函数文件fun.m
function y=fun(x)
y=x.^3-x-1;
主文件main.m
x=1:0.001:1.5;
x=1:0.001:1.5;
a=1;
b=1.5;
plot(x,fun(x),'k')
grid
hold on
eps=0.5*10^(-3);
num=0;
N=50;
while(abs(a-b)>eps && num<N )
c=(a+b)./2
a
b
if(fun(a)*fun(c)<=0)
b=c;
else
if(fun(c)*fun(b)<=0)
a=c;
end
end
num=num+1
plot(c,fun(c),'r*')
fun(c)
text(c,fun(c),num2str(c))
end