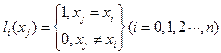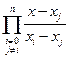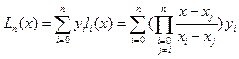插值方法——Lagrange插值公式

问题

已知f(x)=e^x(3x-e^x)，利用插值节点x₀=1.00，x₁=1.02，x₂=1.04，x₃=1.06，构造三次Lagrange插值公式，由此计算f(1.03)的近似值，并给出其实际误差。

原理

根据线性插值和抛物线插值的基函数构造方法，令

其中(i=0,1,..n)为n次多项式，满足

可得：=

则：

根据上面知识可以得到本题的公式

误差：

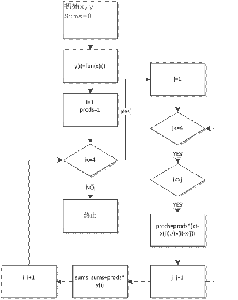
程序框图

结果比较

误差：

结论

1. 误差为 这个单位级别可以忽略。

2. =。所以插值方法算出来基本接近原值。

附件：程序

函数文件fun.m

function y=fun(x)

y=exp(x)*(3*x-exp(x));

主文件main.m

x=[1.00,1.02,1.04,1.06]; %

xt=1.03;

y=[0 0 0 0];

for i=1:4

y(i)=fun1(x(i)); %f(xi)值

end

sums=0;

for i=1:4

prods=1;

for j=1:4

if(i~=j)

prods=prods*(xt-x(j))./(x(i)-x(j)); %联加

end

end

sums=sums+prods*y(i); %联乘

end

sums

fun1(xt)