一.实验目标
掌握最小二乘法求解(无惩罚项的损失函数)、掌握加惩罚项(2范数)的损失函数优化、梯度下降法、共轭梯度法、理解过拟合、克服过拟合的方法(如加惩罚项、增加样本)
二.实验要求和实验环境
实验要求
- 生成数据,加入噪声;
- 用高阶多项式函数拟合曲线;
- 用解析解求解两种loss的最优解(无惩罚项和有惩罚项)
- 优化方法求解最优解(梯度下降,共轭梯度);
- 用你得到的实验数据,解释过拟合。
- 用不同数据量,不同超参数,不同的多项式阶数,比较实验效果。
- 语言不限,可以用matlab,python。求解解析解时可以利用现成的矩阵求逆。梯度下降,共轭梯度要求自己求梯度,迭代优化自己写。不许用现成的平台,例如pytorch,tensorflow的自动微分工具。
实验环境
- Microsoft win10 1809
- python 3.7.0
- Sublime Text 3
三.设计思想
1.算法原理
(0)数据的产生
- x为 之间的随机数.
- 噪音由一个标准正态分布函数 *0.1 产生
- y = sin(x) +
- 利用循环, 根据x产生范德蒙德矩阵X
- 将 X, y 都转为矩阵类型
(1) 解析解(不带惩罚项)
误差函数:
将上式写成矩阵形式:
通过将上式求导我们可以得到式
令 得到
(2) 解析解(带惩罚项)
为了防止参数多时具有较大的绝对值,即过拟合。在优化目标函数式中增加的惩罚项,因此我们得到了:
同样我们可以将上式写成矩阵形式, 我们得到:
对上式求导我们得到:
令 我们得到, 为单位阵。
(3)梯度下降法
若在点可微且有定义,顺着梯度的反方向 即为下降最快的方向。
在不断迭代的过程中, w会走向极值点, 此时为极小值.
判断是否接近极值点在于两次迭代的差值是否足够小;
若后一次迭代比前一次迭代的loss更大则说明要减少学习率.
(4)共轭梯度法求解最优解
共轭梯度法解决形如的线性方程组解的问题 (必须是对称的、正定的)。
共轭梯度法是一个典型的共轭方向法,它的每一个搜索方向是互相共轭的,而这些搜索方向d仅仅是负梯度方向与上一次迭代的搜索方向的组合,因此,存储量少,计算方便。
对于第k步的残差,我们根据残差去构造下一步的搜索方向,初始时我们令。然后利用方法依次构造互相共轭的搜素方向,具体构造的时候需要先得到第k+1步的残差,即,其中如后面的式。
根据第k+1步的残差构造下一步的搜索方向,其中。
然后可以得到,其中
2.算法的实现
(0)数据的产生
x0 = np.random.random((data_size,1)) * data_range
x0 = np.sort(x0,0) # 按列排序, 便于画图
loss = np.random.randn(data_size,1) * 0.1 # 以标准的正态分布*0.1产生噪音
y = np.sin(x0) + loss
return np.matrix(x0),np.matrix(y)
(1) 解析解(不带惩罚项)
w = (x.T * x).I *x.T * t(2) 解析解(带惩罚项)
w = (x.T * x + lamb * np.eye(m) ).I *x.T * t(3) 梯度下降法
while abs(loss1 -loss0) > 1e-8: # 当两次loss相差不大时, 表示接近极值点了.
count +=1
w = w - learning_rate * gradient # 注意此处
loss0 = loss1
loss1 = loss_function(x,y,w)
# 若发现迭代过程中loss变大, 则减小学习率
if np.all(loss1-loss0>0):
learning_rate *= 0.5
gradient = gradient_function(x,y,w)
return w
(4) 共轭梯度法
while not np.all(np.absolute(gradient) <= 1e-3):
count +=1
w = w - learning_rate * gradient # 注意此处
error1 = error_function(x,y,w)
if np.all(error1-error>0):
learning_rate *= 0.5
gradient = gradient_function(x,y,w)
if count >10000:
print(gradient)
count -= 10000
print(count)
return w
四、实验结果与分析
(1) 解析解(不带惩罚项)
(1.1)固定训练集大小, 改变阶数
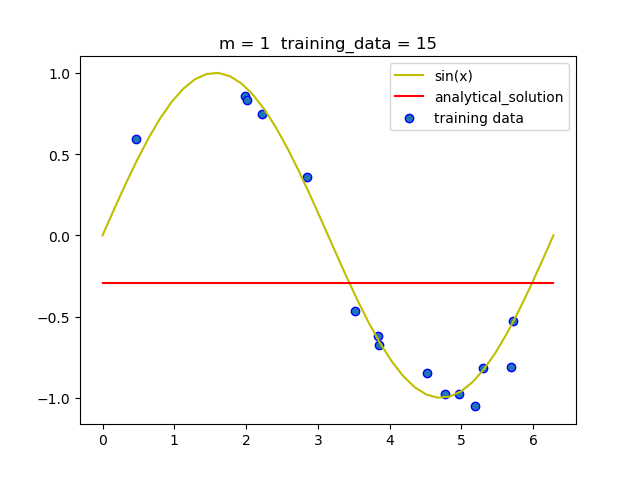
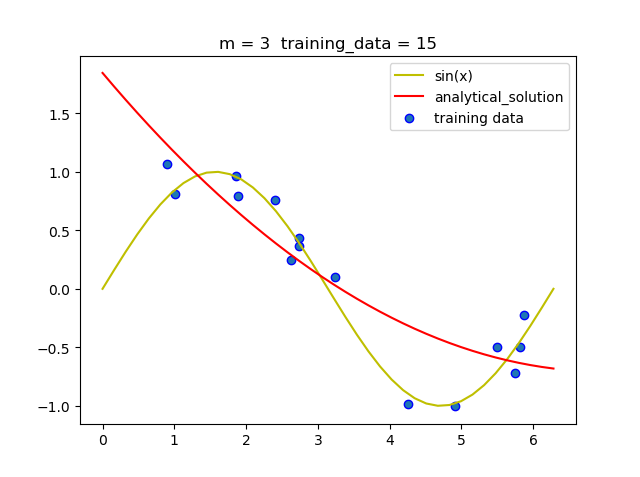
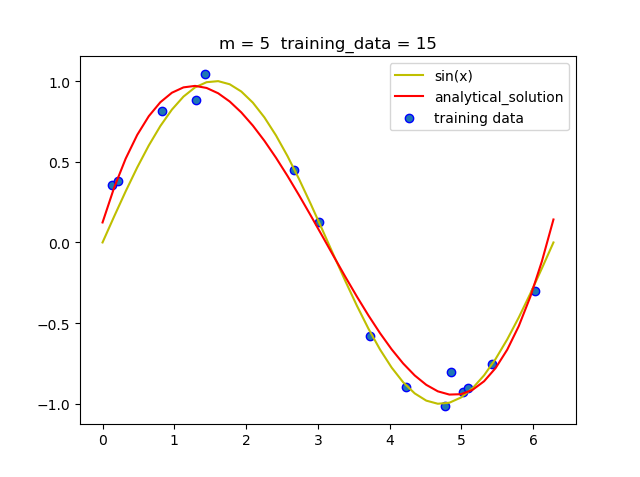
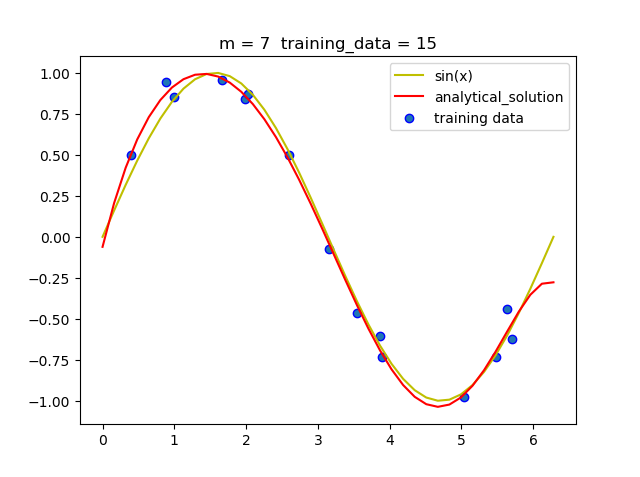
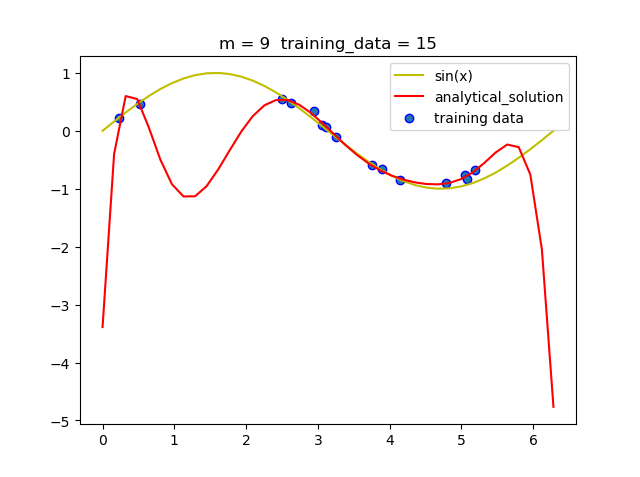
可以看到当m = 5时就拟合的曲线就已经比较准确了, 但当m = 9时, 即使拟合的曲线经过了所有的点, 但和真实曲线相比差距很大, 即发生了过拟合现象.
(1.2)下用loss函数说明过拟合:
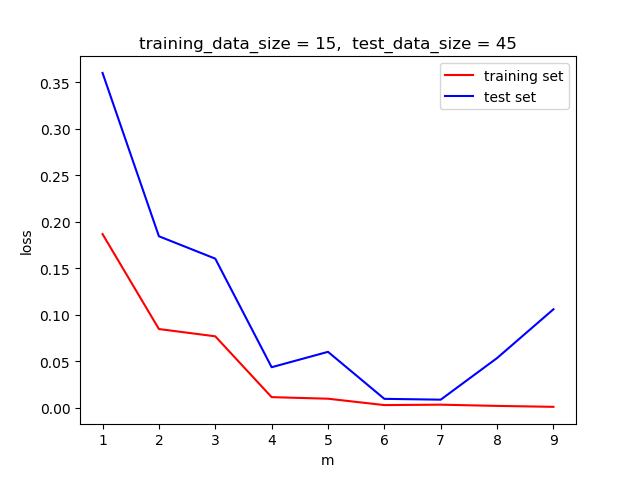
我们选择部分数据用来训练模型, 然后用训练出的模型在新数据上做测试, 观察在不同阶时, loss函数在训练集和测试集上的区别.
如下图, 当m >7时,训练集的loss 仍然保持减小的趋势, 但测试集的loss开始增大, 说明了该模型此时过拟合,已经失去了泛化能力.
(1.3)固定阶数 改变训练集大小
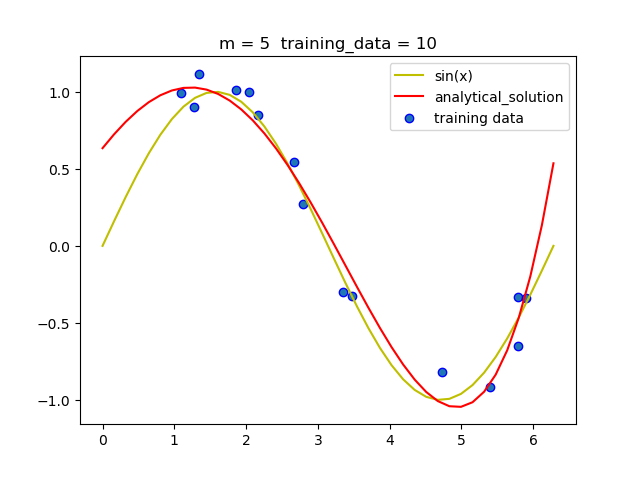
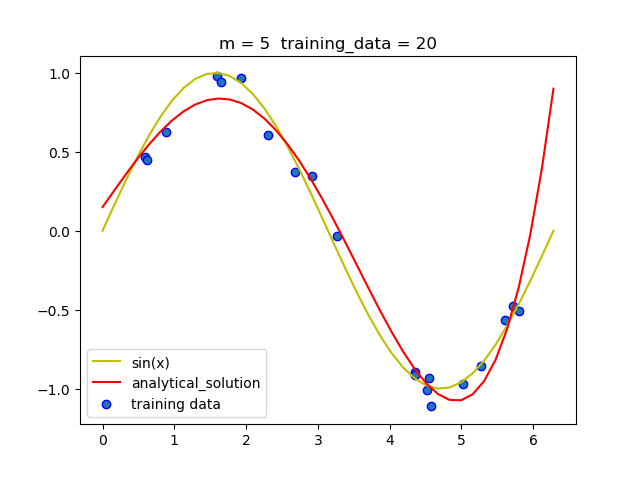
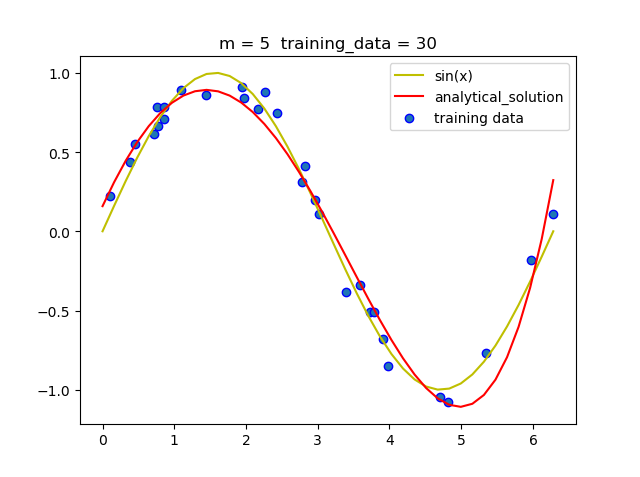
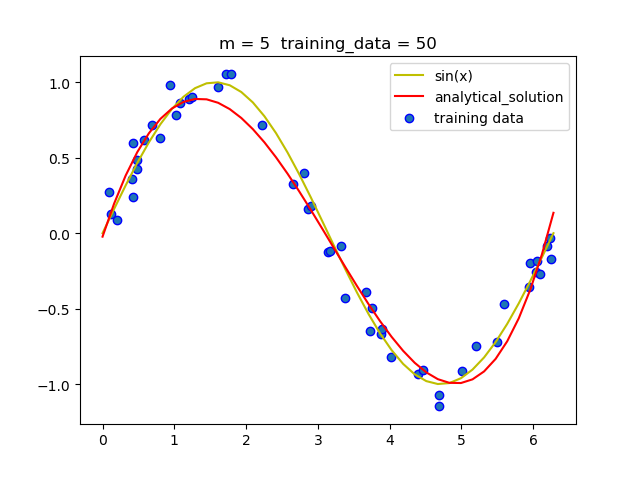
可以看到当阶数固定时, 随着训练集的增大, 拟合的曲线越来越准确.这是因为大量数据可以减少噪声带来的负面影响, 从而减小过拟合情况的发生.
(2) 解析解(带惩罚项)
(2.1) 确定超参数
为了确定最佳的超参数,我们需要通过根均方(RMS)误差来确定,其中RMS的定义如下
将取不同的值代入, 多次实验观察最小根均方误差对应的值,
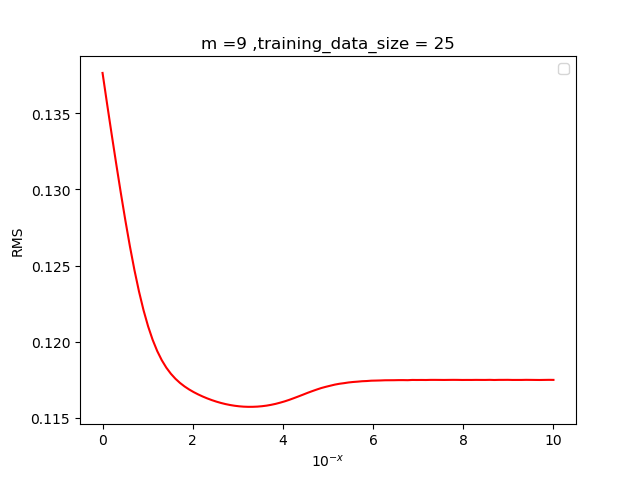
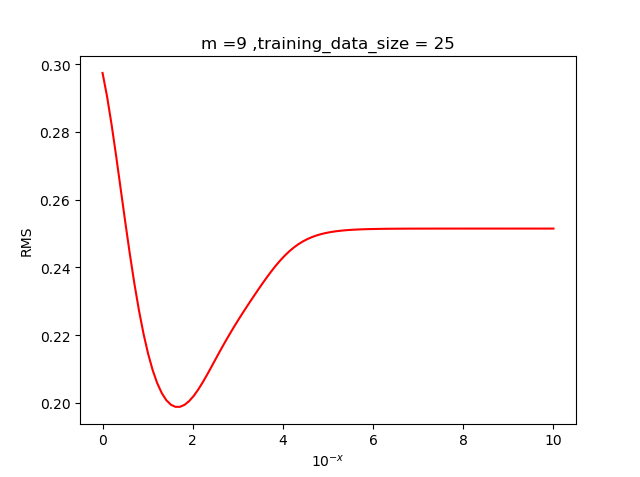
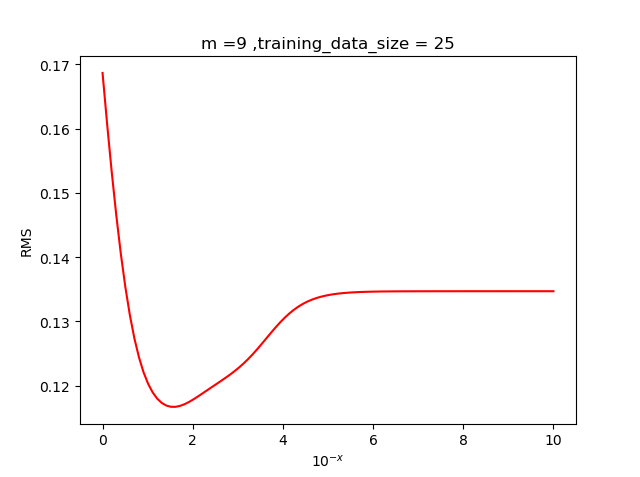
我们发现当超参值在左右效果较好, 于是我们取.
(2.2) 不同阶的拟合情况
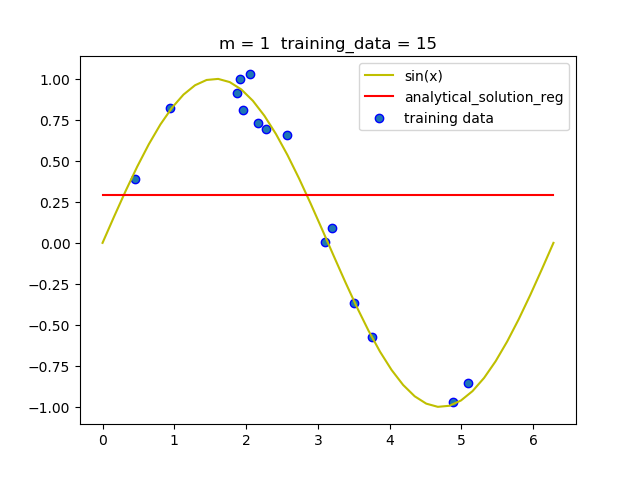
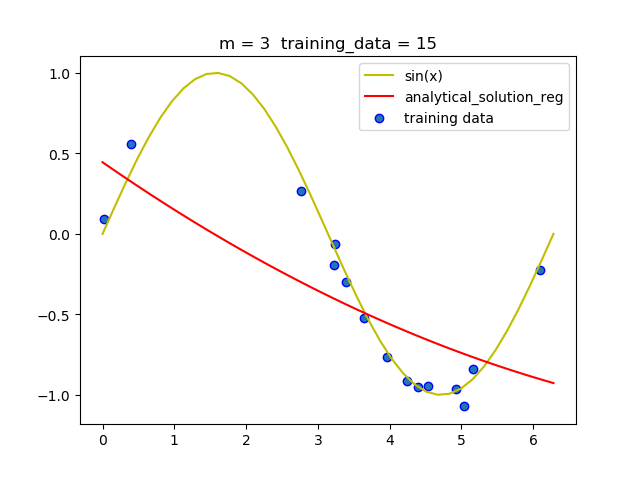
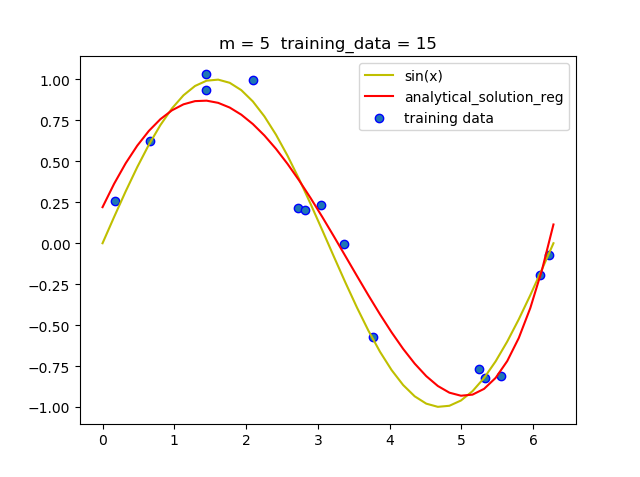
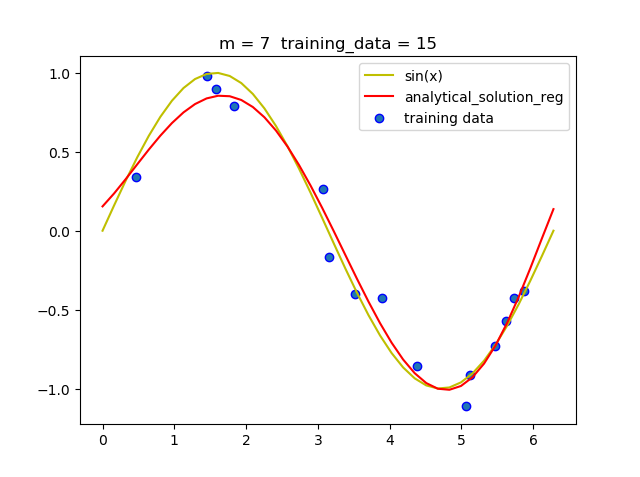
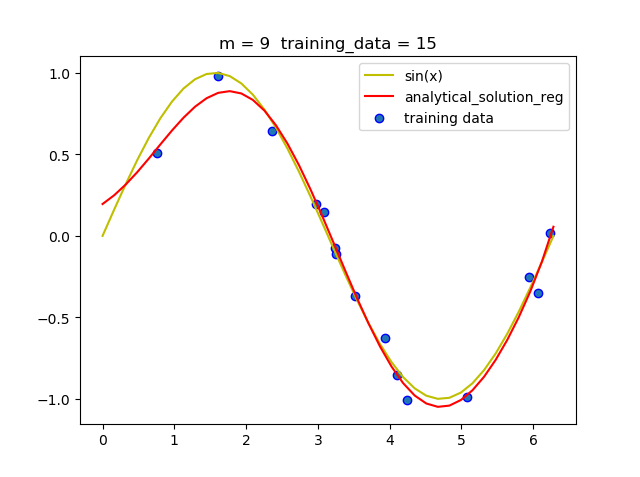
可以看到,带惩罚项的解析解在m = 9 时并没有发生明显的过拟合, 说明带惩罚项可以减少过拟合现相的发生.
根据上述结果解释: 为什么会发生过拟合?
由于训练集中的数据有限,并且数据附带一定的噪声.随着阶数的上升, 模型的表达能力增强, 能够越来越准确的描述训练集中的数据, 为了准确描述这些有噪声的数据, 参数的部分项会非常大,.虽然此时模型准确的表达了训练集, 但这也意味着它将训练集中所有噪声都接纳进来了, 此举不利于模型描述训练集之外的数据,即此时模型的泛化能力将变的很差.
为什么增加惩罚项会有效防止过拟合?
将正则项加入损失函数的方法后, 若参数中部分项过大, 那么损失函数的值就会很大, 为了取得损失函数的极小值, 那么就需要取一个范数较小的值, 而这正好可以有效抑制过拟合.
为什么增加训练集的规模可以有效防止过拟合?
当训练集规模增加时, 模型可以根据更多的数据来不断的改进自己, 使自己更准确,泛化能力更强.
同时, 由于噪声是随机产生的, 大量数据可以降低一些噪声较大数据带来的负面影响.
(3) 梯度下降法
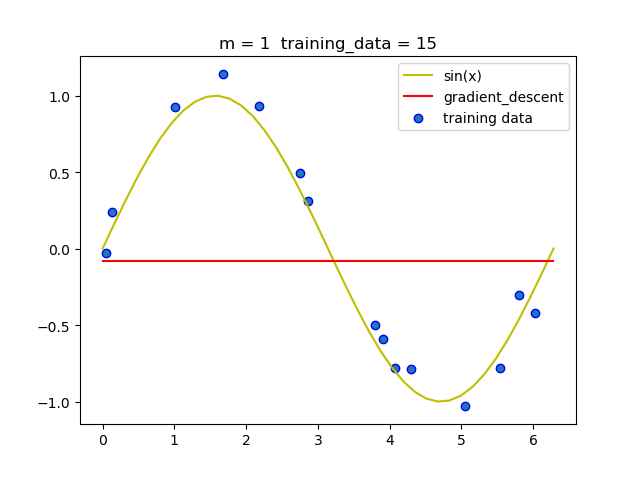
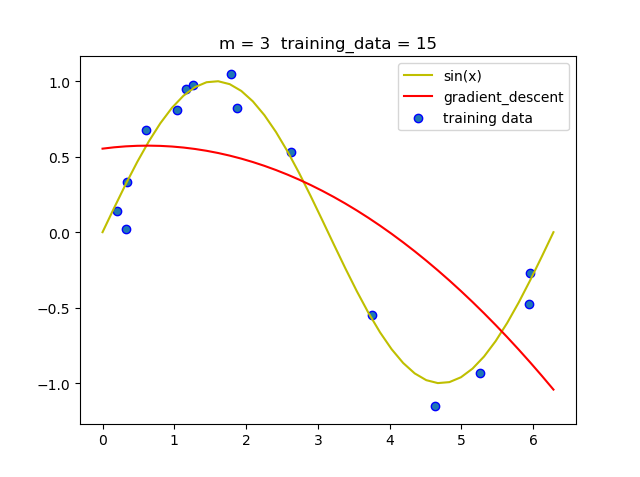
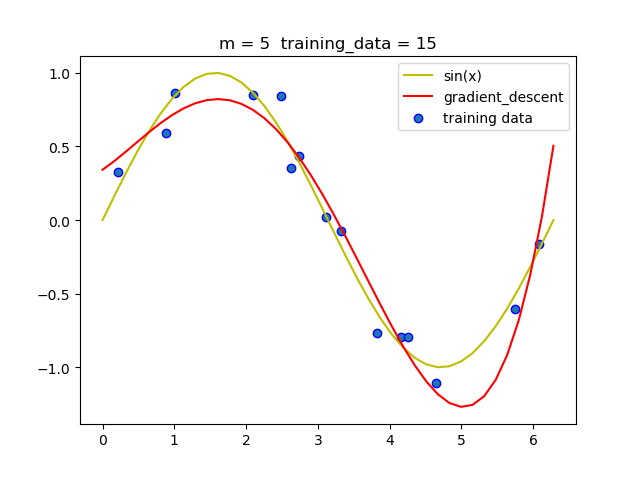
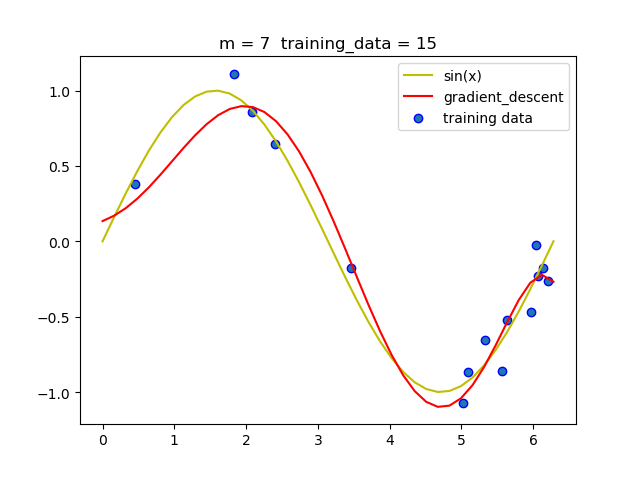
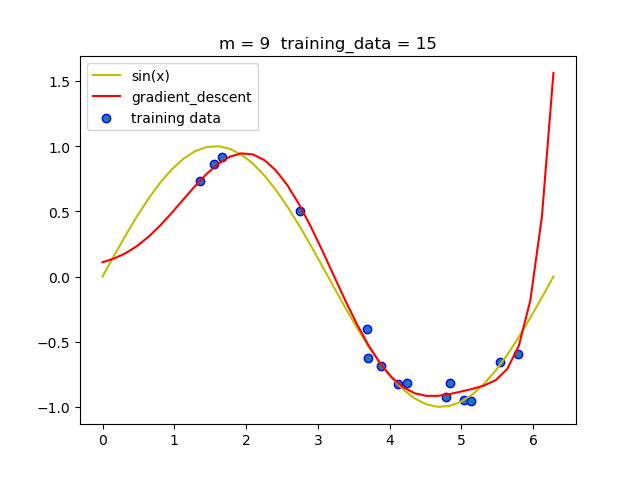
在实验的过程中我发现随着m的增加, 梯度下降法必须要减小学习率, 否则很容易导致无法收敛.
当然在梯度下降法运行的过程中我们需要动态的调节学习率,如过后一次迭代的loss比前一次的loss大,那么就必须将学习率减半.
如下:
# 若发现迭代过程中loss变大, 则减小学习率
if np.all(loss1-loss0>0):
learning_rate *= 0.5若果两次迭代的loss差值小于一个指定的很小的数, 那么我们认为此时非常接近极值点, 可以停止迭代了.
(4) 共轭梯度法
| 阶数 | 迭代次数 |
|---|---|
| 1 | 0 |
| 3 | 2 |
| 5 | 4 |
| 7 | 6 |
| 9 | 8 |
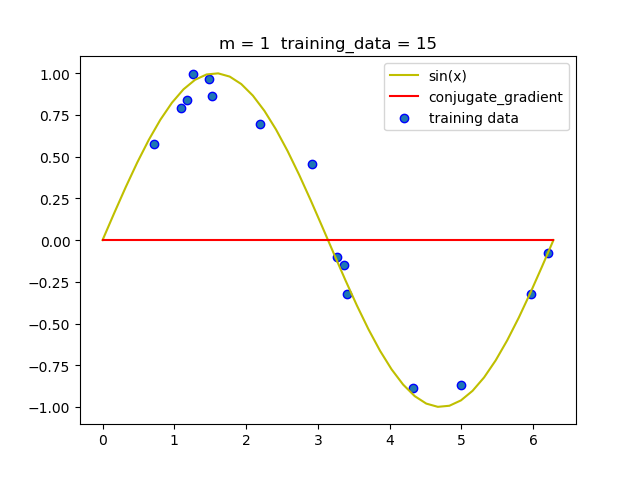

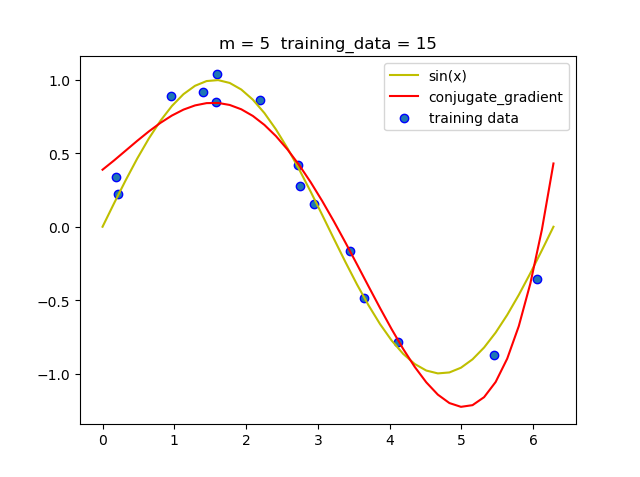
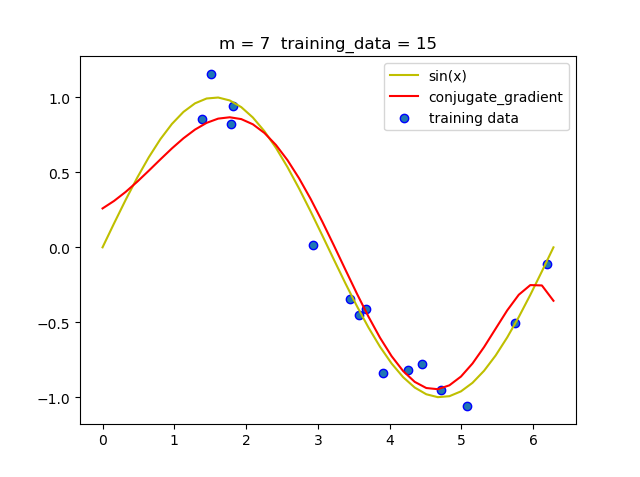
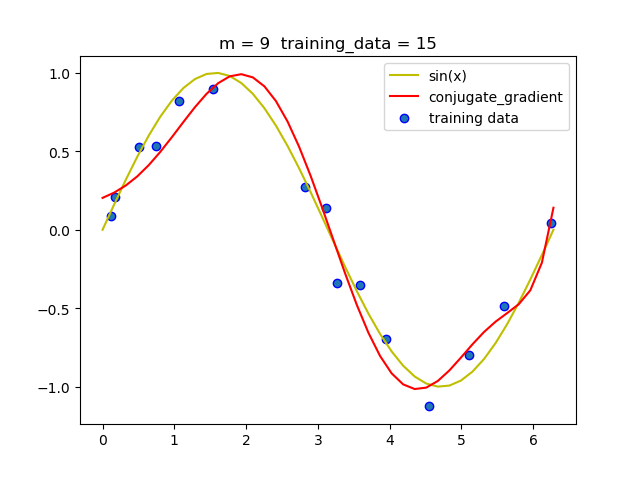
从上述表中我们可以看到, 共轭梯度法迭代非常快, 只需要几次就可以迭代出结果.
五、结论
- 解析解中加入惩罚项可以有效的防止过拟合.
- 增加训练集的数据规模可以有效地防止过拟合.
- 和梯度下降法相比, 共轭梯度法更快,迭代次数更少, 而且结果更准确.
- 在梯度下降法中, 选择合适的学习率很重要, 学习率过小, 迭代次数就会很大, 迭代时间很长.学习率过大, 就可能无法收敛, 或者得到错误的结果.
- 在带有惩罚项的解析解中, 选择合适超参才能使模型更准确.
六、参考文献
- http://cs229.stanford.edu/syllabus.html
- Pattern Recognition and Machine Learning.
- https://baike.baidu.com/item/共轭梯度法/7139204?fr=aladdin
七、附录:源代码(带注释)
# ML-lab1.py
# author 李国庆 1170300523
# time 2019/9/18
# theme 曲线拟合多项式
import numpy as np
import math
import matplotlib.pyplot as plt
# 全局变量
m = 9 # 拟合阶数
data_size = 30 #训练集规模
data_range = math.pi * 2 # x的范围[0,data_range]
lambd = 0.01 # 超参数,用于惩罚项中
learning_rate = 0.0001 # 学习率, 用于梯度下降
method_name = '' # 选择方法
# 主函数
def main():
# 生成数据
x0, y = generate_data()
x = Vandermonde_x(x0)
# 以下是四种方法
global method_name
method_name_set = ['analytical_solution','analytical_solution_reg',
'gradient_descent','conjugate_gradient']
method_name = method_name_set[1] # 从列表中选择方法, 选2时较慢(梯度下降)
if method_name == 'analytical_solution':
w = analytical_solution(x,y)
elif method_name == 'analytical_solution_reg':
w = analytical_solution_reg(x,y)
elif method_name == 'gradient_descent':
w = gradient_descent(x,y,learning_rate)
else:
w = conjugate_gradient(x,y)
test(x0,y,w) # 测试w的拟合情况
# 以sin(x)生成数据,附带噪声
def generate_data():
x0 = np.random.random((data_size,1)) * data_range
x0 = np.sort(x0,0) # 按列排序, 便于画图
loss = np.random.randn(data_size,1) * 0.1 # 以标准的正态分布*0.1产生噪音
y = np.sin(x0) + loss
return np.matrix(x0),np.matrix(y)
# 生成范德蒙德行列式
def Vandermonde_x(x0):
x = np.ones((data_size,1))
for i in range(1,m):
x = np.hstack((x,np.power(x0,i)))
return np.matrix(x)
# 解析解(不带惩罚项)
def analytical_solution(x,y):
w = (x.T * x).I * x.T * y
return w
# 解析解(带惩罚项)
def analytical_solution_reg(x,y):
w =(x.T * x + lambd * np.eye(m)).I * x.T * y
return w
# 梯度函数
def gradient_function(x, y, w):
return (1.0/m) *( x.T * x * w - x.T * y + 0.001 * w)
# 损失函数 loss
def loss_function( x, y, w):
diff = x * w - y
loss = 1.0/(2*data_size)*(diff.T * diff)
return loss[0,0]
# 梯度下降法
def gradient_descent(x, y,learning_rate):
w = np.zeros((m,1))
gradient = gradient_function(x,y,w)
loss0 = 0
loss1 = loss_function(x,y,w)
count = 0
xw = np.linspace(0,2*math.pi,40)
while abs(loss1 -loss0) > 1e-8: # 当两次loss相差不大时, 表示接近极值点了.
count +=1
w = w - learning_rate * gradient # 注意此处
loss0 = loss1
loss1 = loss_function(x,y,w)
# 若发现迭代过程中loss变大, 则减小学习率
if np.all(loss1-loss0>0):
learning_rate *= 0.5
gradient = gradient_function(x,y,w)
# 每1000次迭代绘一次图
if count >1000:
print(loss1-loss0)
count -= 1000
yw = np.polyval(w[::-1],xw)
plt.scatter(x[:,1].tolist(),y.tolist(),edgecolor="b")
plt.plot(xw,yw,'r')
plt.pause(0.001)
plt.clf()
return w
# 共轭梯度法
def conjugate_gradient(x, y):
lambd = 0.001
Q = (1 / m) * (x.T * x + lambd * np.mat(np.eye(x.shape[1])))
w = np.mat(np.zeros(x.shape[1])).T
r = -gradient_function(x, y, w)
p = r
count = 0
for i in range(1, x.shape[1]):
count += 1
a = float((r.T * r) / (p.T * Q * p))
r_prev = r
w = w + a * p
r = r - a * Q * p
p = r + float((r.T * r) / (r_prev.T * r_prev)) * p
return w
# 测试效果
def test(x0,y,w):
# 画出给定点的散点图
plt.scatter(x0.tolist(),y.tolist(),edgecolor="b", label="training data")
# 画出结果的模拟曲线
xw = np.linspace(0,2*math.pi,40)
yw = np.polyval(w[::-1],xw)
plt.plot(xw,np.sin(xw),'y',label = 'sin(x)')
info = 'm = '+ str(w.shape[0])+' training_data_size = '+str(data_size)
plt.plot(xw,yw,'r',label = method_name)
plt.legend()
plt.title(info)
plt.show()
if __name__ == '__main__':
main()