算法分析的数学基础

第2章 算法分析的数学基础

《Introduction to Algorithms》
 第三章 第四章 附 录

一. 计算复杂性函数的阶

计算函数的阶:

1. 算法执行时间随问题规模增长而增长的阶（增长率).
2. 执行时间函数的主导项

如: $T(n)=an^2 +bn+c$

主导项: $an^2$,当输入大小n较大时，其它低阶项相对来说意义不大,系数a也相对来说意义不大

即：函数T(n)的阶为n 2

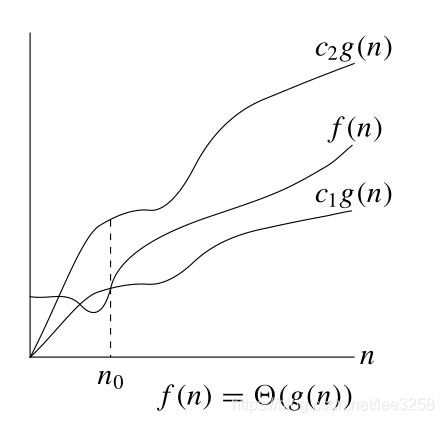
定义(同阶): 设f(n)和g(n)是正值函数。如果
$exist c1 , c 2 >0, n_0 , forall n>n_0 , c_1 g(n) le f(n) le c_2 g(n)$，则称f(n)与g(n)同阶，记作f(n)= $heta$(g(n)) 。

证明同阶,找到n ,c1, c2使得他们满足定义

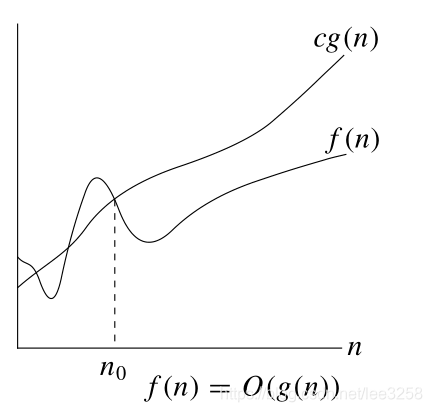
定义(低阶) 设f(n)和g(n)是正值函数。如果$ exist c>0, n_0 , forall n>n_0 , f(n)le cg(n)$，则称f(n)比g(n)低阶或g( n )是 f ( n ) 的 上 界 ， 记 作 f ( n ) = O ( g ( n ) ) 。

证明低阶: 找到n ,c满足定义

O ( g ( n ) ) 代表复杂度上界是g(n), f ( n ) = O ( g ( n ) )代表f(n)的复杂度小于g(n),读作复杂度不超过g(n)

如果$f(n)=O(n^k )$, 则称f(n) 是多项式界限的

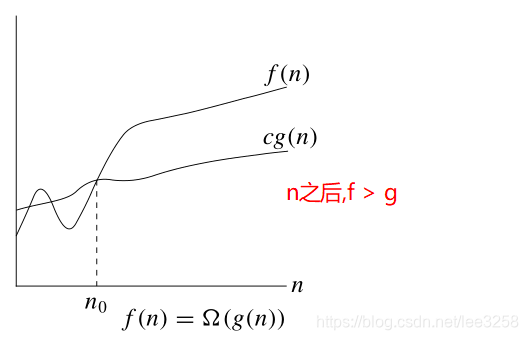
定义(高阶) 设f(n)和g(n)是正值函数。如果$exist c>0, n_0 , forall n>n_0 , f(n) ge cg(n)$，则称f(n)比g(n)高阶或g(n)
是f(n)的下界，记作f(n)= $Omega$ (g(n)) 。

证明高阶: 找到 n ,c 满足定义

$Omega$ (g(n))代表复杂度下界为g(n), 读作复杂度不低于g(n)

对于插入排序，我们可以说

– 最好运行时间是$Omega $(n) – 或者说，运行时间是$Omega $(n) – 插入排序算法的运行时间在$Omega $(n)和 O(n 2 )之间 – 插入排序算法的最坏运行时间是$Omega $(n 2 ) – 但说插入排序算法的运行时间是$Omega $(n 2 )，是错误的！

定义(严格低阶). 设f(n)和g(n)是正值函数。如果
$forall c>0, exist n_0 , forall n>n 0 , f(n)<cg(n)$，则称f(n)严格比g(n)低阶或g(n)是f(n)的严格上界，记作f(n)=o(g(n)) 。

定义(严格高阶). 设f(n)和g(n)是正值函数。如果$forall c>0, exist n_0 , forall n>n_0 , f(n)>cg(n) $，则称f(n)严格比g(n)高阶或g(n)是f(n)的严格下界，记作f(n)= $omega$ (g(n)) 。

$ heta $**(g(n))可以视为所有与g(n)同阶的函数集合 **

O(g(n))可以视为所有比g(n)低阶的函数的集合

$Omega $ (g(n))可以视为所有比g(n)高阶的函数集合

o(g(n))可以视为所有比g(n)严格低阶的函数集合

$omega $ (g(n))可以视为所有比g(n)严格高阶的函数集合

注意,并不是所有函数的阶都是可比的

函数阶的性质

自反性

对称性

传递性

反对称性

二. 和式的估计与界限

1.线性和

$sum^n(ca_k+b_k) = csum^n a_k+sum^nb_k$

$sum_{k=1}^n heta(f(k)) = hetasum^n_{k=1} f(k)$

2.级数

$sum_{i=1}^n i =frac{n(n+1)}{2} = heta(n^2)$

$sum_{k=0}^n x^k = x^0+x^1+x^2+dots+x^n =frac{x^{n+1}-1}{x-1} \ sum_{k=0}^infin x^k = frac{1}{1-x} |x<1|$

$H_n = sum_{k=1}^nfrac{1}{k} = ln n+O(1)$

$sum_{k=1}^n a_k - a_{k-1} = a_n -a_0$

$sum_{k=0}^{n-1} a_{k} - a_{k+1} = a_0 -a_n$

$sum_{k=1}^{n-1}frac{1}{k(k+1)} = 1 - frac{1}{n}$

$lg(prod_{k=1}^{n}a_k) = sum_{k=1}^nlg a_k$

三. 递归方程

递归方程: 递归方程是使用具有小输入值的相同方程来描述一个方程.用自身来定义自身.

解递归方程的3种方法:

1. 替换方法:
   – 先猜测方程的解,
   – 然后用数学归纳法证明 .
2. 迭代方法:
   循环地展开递归方程，
   把递归方程转化为和式，
   然后可使用求和技术解之
3. Master方法:
   – 求解型为T(n)=aT(n/b)+f(n)的递归方程

Master方法

目的: 求解$T(n) = aT(n/b)+f(n)$类型的方程, 要求a >=1 ,b >1 是常数, f(n)是正函数

比较$f(n) 和 g(n) = n^{lg_ba} $的大小

1. 若f(n) > g(n),则$T(n) = heta (f(n))$ , 且存在c (c<1),n’使得 af(n/b) <= cf(n)在n>n’时恒成立.

2. 若f(n) < g(n),则$T(n) = heta (g(n))$

3. 若f(n),g(n)同阶,则$T(n) = heta (f(n)log n)$