1.背景
大家在使用JMeter进行性能测试时,聚合报告(Aggregate Report)可以说是必用的监听器,但是你真的了解聚合报告么?
2.目的
本次笔者跟大家聊聊聚合报告(Aggregate Report)常用误区。
3.常见误区
说明:本次笔者采用的JMeter版本为5.1.1
- 误区一:90%、95%、99百分位的理解
经常有的同学理解成平均90%、95%、99%请求的交易耗时,包括一些做了很久的老测人员试竟然也是这么理解的(其实笔者最开始也是这么理解的),出现这个问题根本原因是对百分位的概念理解错误(换句话说:你数学是体育老师教的吧!),那么正确该怎么理解呢?
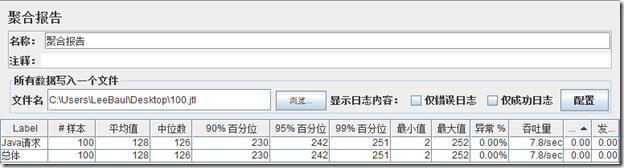
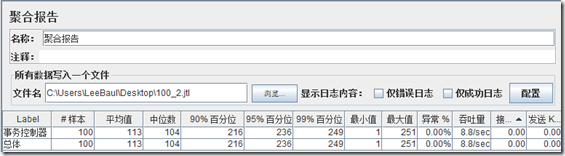
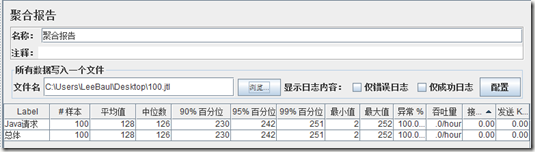
我们来看一张聚合报告图:
正解:90%百分位值为230ms,在发送100笔请求过程中,聚合报告会实时给请求耗时进行由小到大行排序,排序后的第90个请求耗时为230ms,也就是说前90笔请求中耗时最长的是230ms(其余90%百分位,95%百分位道理类似就不占篇赘述了),聚合报告平均值要与百分位值结合来看。
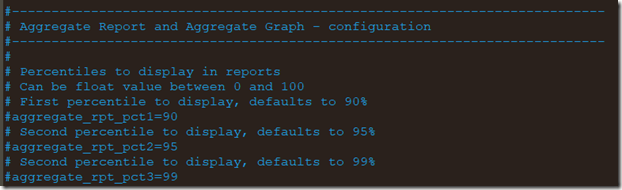
说明:90%、95%、99%值是支持自定义在jmeter.properties修改:
- 误区二:把吞吐量值当TPS值
经常有的同学直接把聚合报告中的吞吐量当作TPS来看(网上还有一种说法是把请求放在事务控制器里,吞吐量就可以看成TPS,经笔者验证并不可以),这种做法是相当不严谨的。那么聚合报告中的吞吐量什么情况下可以看成TPS?
老规矩还是用实际操作来验证:
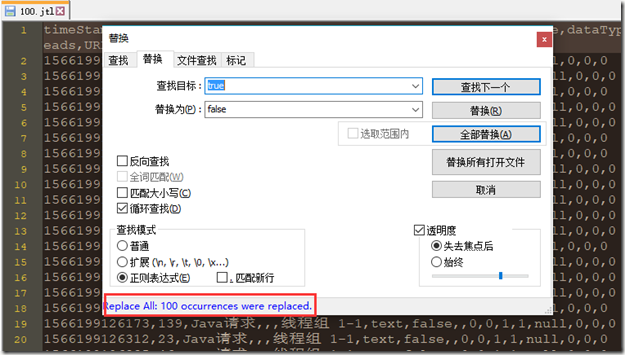
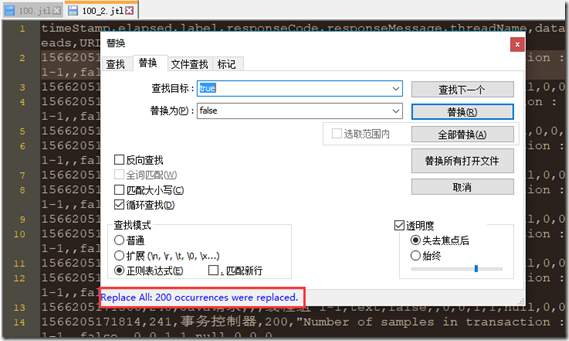
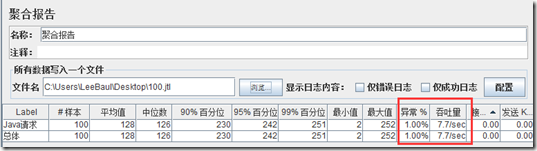
没错,还是上面聚合报告的图,笔者把100.jtl文件中的请求全部改成false,再来看下聚合报告结果:
然后再用聚合报告打开100.jtl结果文件,聚合报告各项数据没有任何改变(笔者就不放图了,不然就一张图用了3遍),笔者这种做法是比较极端的(或者可以说笔者把现象放大了),此时再把吞吐量看成TPS就出事了。。。。请求全失败了,TPS应该是0吧?????
给大家举个栗子,大家都看过赵本山大叔的《钟点工》小品,里面有个经典的问题:把大象关进冰箱需要几步?相信大家都知道答案。我们换种思维:假如我们把这个操作看成一个事务,如果找不到大象,或者没有冰箱,这个事务都是无法完成的,也就是说这个事务最终会失败(事务只有两种状态要么成功要么失败)。
那么什么时候吞吐量可以成TPS,从严格意义来讲就是交易成功率为100%;还有一种情况是:交易失败率在你可以接受的范围内(对当前测试整体结果影响不大,到了可以忽略的程度)。
我们再来验证下网上说的方法吧:把请求放在事务控制器里
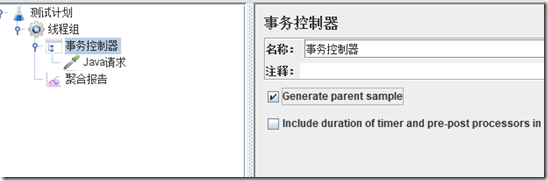
脚本结构图:
有的同学可以能会问:事务控制器为啥不放多个请求,其实从本质上看是没这个必要的,放多个请求也不影响最终结果。
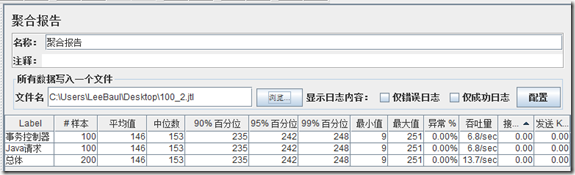
笔者还是用之前的操作把100_2.jtl中的请求全部改成false,再来看下聚合报告结果:
聚合报告结果图(为什么会总体样本会是200,笔者觉得问题出在逆向解析过程中会把JTL结果文件中所有的样本解析出来):
吞吐量的值还是没有变,此时吞吐量值预期结果应该是零,进而证明网上的所谓的套路不靠谱(感觉网上说的增加事务控制器的,目的更偏向与如何把多个请求组装成一个事务,这也是事务控制的作用)。
4.JMeter聚合报告源码优化
针对以上问题,笔者查看了聚合报告底层源码,总结下:聚合报告是无状态的(状态是样本的状态),只负责统计数据(就是个计数器),统计时只认Sampler的Label,笔者个人感觉源生的聚合报告,不是十分合适OLTP。
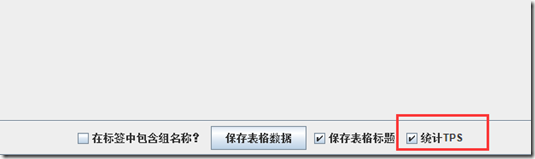
笔者优化了:统计计算公式,支持GUI页面控制(默认勾选统计tps,如果不勾选则还是统计吞吐量)
再看下100.jtl结果文件全部false效果:
笔者手动改下100.jtl改成只失败1笔,执行结果如下: