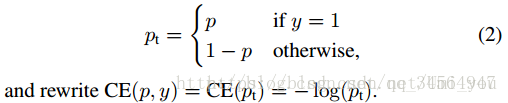转自:https://blog.csdn.net/Umi_you/article/details/80982190
Focal loss 出自何恺明团队Focal Loss for Dense Object Detection一文,用于解决分类问题中数据类别不平衡以及判别难易程度差别的问题。文章中因用于目标检测区分前景和背景的二分类问题,公式以二分类问题为例。项目需要,解决Focal loss在多分类上的实现,用此博客以记录过程中的疑惑、细节和个人理解,Keras实现代码链接放在最后。
框架:Keras(tensorflow后端)
环境:ubuntu16.04 python3.5
二分类和多分类
从初学开始就一直难以分清二分类和多分类在loss上的区别,虽然明白二分类其实是多分类的一个特殊情况,但在看Focal loss文章中的公式的时候还是不免头晕,之前不愿处理的细节如今不得不仔细从很基础的地方开始解读。
多分类Cross Entropy:
二分类Cross Entropy:
可以看出二分类问题的交叉熵其实是多分类扩展后的变形,在FocalLoss文章中,作者用一个分段函数代表二分类问题的CE(CrossEntropy)以及用pt的一个分段函数来代表二分类中标签值为1的 部分(此处的标签值为one-hot[0 1]或[1 0]中1所在的类别):
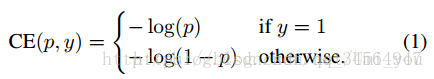
文章图中的p(predict或probility?)等价于多分类Cross Entropy公式的y,也即经激活函数(多分类为softmax函数,二分类为sigmoid函数)后得到的概率,而文章中的y对应的是Cross Entropy中的,即label。
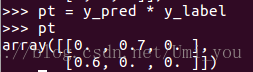
CE经分段函数pt作为自变量后可以转化为,实际上所代表的就是多分类CE中的(标签值)为1对应的的值,只不过在二分类中和互斥(两者之和为1),所以可以用一个分段的变量来表示在i取不同值情况下的,我理解为当前样本的置信度,越大置信度越大,交叉熵越小。总结:多分类中每个样本的pt为one-hot中label为1的index对应预测结果pred的值,用代码表达就是
了解所代表的是什么之后,接下来多分类的Focal Loss就好解决了。接下来举个三分类的例子来模拟一下流程大致就知道代码怎么写了:
假设
为softmax之后得出的结果:
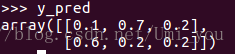
为one-hot标签:
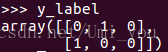
:
:
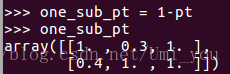
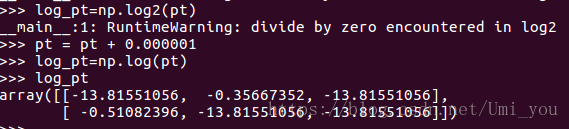
:(注意pt可能为0,log(x)的取值不能为0,所以加上epsilon)
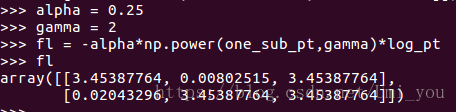
Fl:
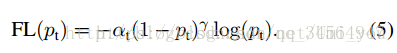
可以看到3.4538..的地方本该是0才对,原因是log函数后会得到一个很小的值,而不是0,所以应该先做log再乘y_label:
原:
改:
顺带一提,在多分类中alpha参数是没有效果的,每个样本都乘以了同样的权重
详细信息可以看代码中的注释
代码:Keras版本