项目地址
https://github.com/Leext/SudokuSolver
解题思路
程序的需求有两个:
- 生成给定数量的数独终局
- 求解给定的数独
对于第一个需求,我直接想到的就是,随机生成一些初始局,再求解不就是数独终局了吗。并且这种方法可以生成任意对初始局有限制的数独。所以核心的问题就转化为求解。
关于求解的思路很容易想到,就是回溯搜索+优化剪枝。
如果是从左往右、从上到下依次搜索每个格子,这样会使需要求解的数量变得比较大。数独每个格子的数字是被行、列、格所限制的,人在玩的时候,总是会根据其他数字的限制先填一个格子。由此可以得到一个剪枝的思路,每当要决定搜索哪个格子的时候,选择可行解最少的。直觉上来说,搜索时每一步的可行解都是最少的,每一次尝试之后,试填的格子周围的可行解数量也都会减少,使得后面的可行解数量也变小。这样就加快了搜索的速度。
对于规定生成的终局左上角为特定数字,由于是求解生成,所以只要初始局满足要求,那生成的所有终局都是满足要求的。
实现过程
实现
代码的整个 设计如下:
SudokuBoard 类:封装了数独棋盘,方法包括:棋盘构建,寻找可行解,计算可行解数量,寻找最小可行解格子
SudokuSolver 类:求解器类,方法包括:验证棋盘,深度优先搜索,生成棋盘,文件读取,求解数独
核心的算法是搜索:
- 计算所有格子的可行解数量
- 如果没有可求解的,则回溯;如果获得一个解,则保存起来,达到一定数量后退出
- 寻找可行解最少的格子作为待解格子
- 获取该格子的所有可行解
- 对于格子的每一个可行解,设置棋盘为该可行解
- 递归搜索(回到1)
对于题目中要求的左上角数字,
单元测试
测试代码如下:
void test()
{
SudokuBoard board = SudokuBoard(std::string("012345678000000000000000000000000000000000000000000000000000000000000000000000000"));
assert((1 << 8) == (board.getFeasible(0, 0) >> 1));
assert(1 == board.countFeasible(0, 0));
board = SudokuBoard(std::string("012345678900000000000000000000000000000000000000000000000000000000000000000000000"));
assert(0 == board.countFeasible(0, 0));
board = SudokuBoard(std::string("012300000400000000507000000000000000000000000600000000000000000600000000000000000"));
assert(2 == board.countFeasible(0, 0));
auto p = board.findFewest();
assert(0 == p.first && 0 == p.second);
board = SudokuBoard(std::string("000000010400000000020000000000050407008000300001090000300400200050100000000806000"));
SudokuSolver solver;
SudokuBoard *b = solver.solve(board);
assert(solver.check(*b));
board = SudokuBoard(std::string("000000010400000000020000000000050604008000300001090000300400200050100000000807000"));
b = solver.solve(board);
assert(solver.check(*b));
board = SudokuBoard(std::string("000000012003600000000007000410020000000500300700000600280000040000300500000000000"));
b = solver.solve(board);
assert(solver.check(*b));
board = SudokuBoard(std::string("000000012008030000000000040120500000000004700060000000507000300000620000000100000"));
b = solver.solve(board);
assert(solver.check(*b));
board = SudokuBoard(std::string("000000012040050000000009000070600400000100000000000050000087500601000300200000000"));
b = solver.solve(board);
assert(solver.check(*b));
board = SudokuBoard(std::string("000000012050400000000000030700600400001000000000080000920000800000510700000003000"));
b = solver.solve(board);
assert(solver.check(*b));
board = SudokuBoard(std::string("000000013000030080070000200000206000030000900000010000600500204000400700100000000"));
b = solver.solve(board);
assert(b == NULL);
solver.generate(board);
solver.generateN(3, board);
copeSolve("a.txt");
copeGenerate("10");
}
测试包括几个构造好的样例来测试可行解有关的函数,然后测试代码是否能正确解题,最后是测试处理命令行时调用函数的正确性。

代码也都全部覆盖(未覆盖的是对于文件读入的异常提示,因为这次作业不会出现这种情况,就没有测试)
性能改进
在初步完成代码以后,我进行了性能分析。以下是生成100万个数独终局时,程序所用的时间分布。由于我的算法生成和求解是等价的,所以生成时的性能可以体现求解的性能。

从中可以发现getBanArray这个函数耗费的时间比较多。
bool *SudokuBoard::getBanArray(int x, int y)
{
bool *banArray = new bool[10];
for (int i = 0; i < 10; i++)
banArray[i] = false;
for (int i = 0; i < 9; i++)
banArray[_board[i][y]] = true;
for (int j = 0; j < 9; j++)
banArray[_board[x][j]] = true;
int start_x = x / 3 * 3;
int start_y = y / 3 * 3;
for (int i = start_x; i < start_x + 3; i++)
for (int j = start_y; j < start_y + 3; j++)
banArray[_board[i][j]] = true;
return banArray;
}
std::vector<int>& SudokuBoard::getSolveVector(int x, int y)
{
bool *banArray = getBanArray(x, y);
std::vector<int>* rtn = new std::vector<int>;
for (int i = 1; i < 10; i++)
if (!banArray[i])
rtn->push_back(i);
delete banArray;
return *rtn;
}
这个函数是我用来获取某个格子的可行解情况的,它使用布尔数组来储存。在另一个函数中还要利用这个布尔数组生成可行解的vector。这个过程非常繁琐。由于我的算法需要大量调用这个函数,所以非常耗时。我改进了这个过程,使用一个int来表示可行解。用int的低位来表示某个数字是否可行。
改进之后这个过程的代码:
int SudokuBoard::getFeasible(int x, int y)
{
int bit = 0;
const int complete = 0x3fe;
for (int i = 0; i < 9; i++)
bit |= 1 << _board[i][y];
for (int j = 0; j < 9; j++)
bit |= 1 << _board[x][j];
int start_x = x / 3 * 3;
int start_y = y / 3 * 3;
for (int i = start_x; i < start_x + 3; i++)
for (int j = start_y; j < start_y + 3; j++)
bit |= 1 << _board[i][j];
return bit^complete;
}
int SudokuBoard::countFeasible(int x, int y)
{
// _board[x][y] must be 0
int bit = getFeasible(x, y) >> 1;
int count = 0;
while (bit)
{
bit &= (bit - 1);
count++;
}
return count;
}
改进之后的性能分析:
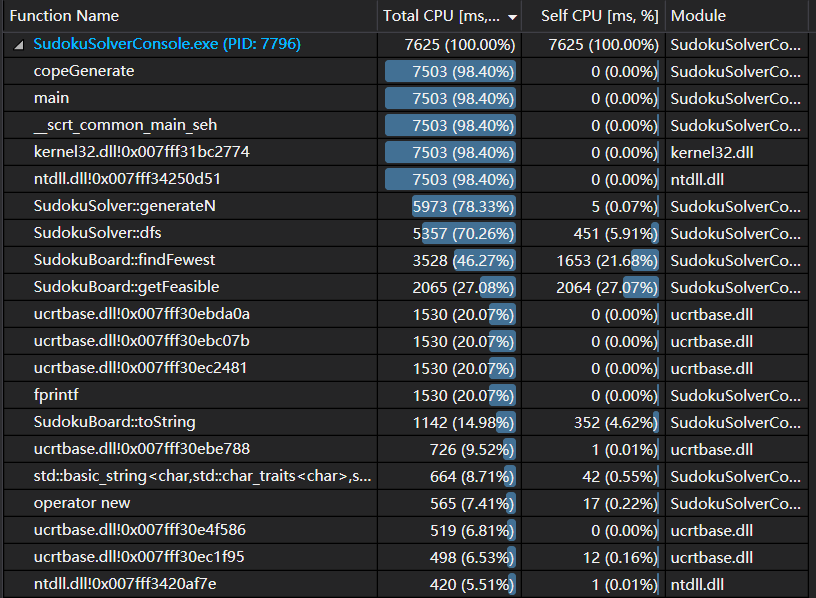
可以看到花费的时间从21.6s减少到了7.6秒,性能提升了60%以上。
进一步可以看到fprintf,即写文件的函数,占用了五分之一的时间。因此我尝试另外开一个线程来完成写入文件,但是不知道是不是我自己实现的问题,这个改进并没有加快速度。
代码说明
关键的代码是搜索求解的函数:
bool SudokuSolver::dfs(SudokuBoard& board)
{
std::pair<int, int>& target = board.findFewest();
if (target.first == -1) // end
{
_solveCount++;
solutions->push_back(board.toString());
return _solveCount >= _solveLimit;
}
if (target.second == -1) // no solution
return false;
int feasible = board.getFeasible(target.first, target.second);
for (int i = 1; i <= 10; i++)
{
if ((feasible >> i) & 1)
{
board.set(target, i);
if (dfs(board))
return true;
}
}
board.set(target, 0);
return false;
}
首先获得可行解最少的格子,findFewest 的结果可以作为是否找到解和解不存在的标识。继续搜索则获取该格子的可行解。for循环遍历每个可行解。for循环结束后,把当前格子置为0。
PSP
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | ||
| · Estimate | · 估计这个任务需要多少时间 | 10 | 15 |
| Development | 开发 | ||
| · Analysis | · 需求分析 (包括学习新技术) | 120 | 150 |
| · Design Spec | · 生成设计文档 | 30 | 30 |
| · Design Review | · 设计复审 (和同事审核设计文档) | 0 | 0 |
| · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | 0 | 0 |
| · Design | · 具体设计 | 30 | 60 |
| · Coding | · 具体编码 | 300 | 500 |
| · Code Review | · 代码复审 | 60 | 100 |
| · Test | · 测试(自我测试,修改代码,提交修改) | 100 | 300 |
| Reporting | 报告 | ||
| · Test Report | · 测试报告 | 60 | 100 |
| · Size Measurement | · 计算工作量 | 30 | 30 |
| · Postmortem & Process Improvement Plan | · 事后总结, 并提出过程改进计划 | 60 | 60 |
| 合计 | 800 | 1345 |
感想
这一次作业我一开始是当成一个OO作业来做的,因为和上学期的OO课作业差不多。但是这一次我开始审视自己的编码过程。
首先对于项目花费时间的估计,我就和实际的有很大偏差。能想到的原因有几个。
一个是我对于C++不太熟悉,因为之前一直写的Java,没有指针的困扰,写着也比较方便。这次写C++踩了一些坑,查了很多资料。
还有就是我在还没有仔细想好组织的时候就开始写了,边写代码边思考架构比较耗时间,因为经常会陷入到C++实现的细节里面去,同时思考不同层次的问题会比较消耗认知资源。。。
最后就是自己的时间管理还是有些问题,有时不太专注。
一个小项目还是能发现自己很多问题的,这大概就是自己选这课的目的吧,走出舒适区暴露自己的问题。