方差分析 | ANOVA | 原理 | R代码 | 进阶 | one way and two way | Analysis of Variance

问题：

• 为什么组间方差加组内方差一定等于总方差？如何从数学上理解。PPT里有证明，引入一个中间项就行。
• 方差分析、协方差分析和回归分析有什么联系？
• 什么是F分布？Fisher的独创，理解不了F分布就不可能真正理解方差分析。
• 方差分析，就是要分析方差的来源！

我们把组内方差看做是随机误差；组间差组成比较复杂：包含了随机误差、系统误差。 

PPT：方差分析----单因素方差分析

回忆一下：

卡方分布就是多个标准正态分布变量平方的和，自由度是其唯一的参数。（为什么当自由度为3时，卡方分布的形状就变了，和三体问题有关吗？）

F分布就是两个不同卡方分布的比的分布，自由度是其唯一的参数（两个自由度而已）。

方差分析假设随机误差是服从正态分布的，那么我们假设组内和组间无差异，很自然就转换到了F分布。

那就连t分布一起回顾吧！t就是学生的意思，著名的t-SNE也是基于t分布的，t分布和正态分布形状基本是一样的，当t分布唯一的参数自由度大于30时，t分布就趋近于正态分布了。普通的z分布底下除的是总体标准差，t分布底下除的是样本标准差。t分布的自由度就是抽样分布中的sample size，根据中心极限定理，sample size越大，抽样分布的均值就越趋近于正态分布。【YouTube上有个视频讲得非常清楚】

原理

比较两组（小样本）就用t-test，比较三组及以上就用ANOVA。注意：我们默认说的都是one way ANOVA，也就是对group的分类标准只有一个，比如case和control（ABCD多组），two way就是分类标准有多个，比如case or control，male or femal。

方差分析的核心原理：组内方差和组间方差是否有明显的差异，用的F统计量，F分布有两个参数，也就是两个自由度参数。

方差分析会给一个总的显著性结果，及组内和组间是否有显著差异。显著了需要再做两两比较。

R实例

One-Way ANOVA Test in R

my_data <- PlantGrowth

# Show a random sample
set.seed(1234)
dplyr::sample_n(my_data, 10)

# Show the levels
levels(my_data$group)

my_data$group <- ordered(my_data$group,
                         levels = c("ctrl", "trt1", "trt2"))

library(dplyr)
group_by(my_data, group) %>%
  summarise(
    count = n(),
    mean = mean(weight, na.rm = TRUE),
    sd = sd(weight, na.rm = TRUE)
  )

# Box plots
# ++++++++++++++++++++
# Plot weight by group and color by group
library("ggpubr")
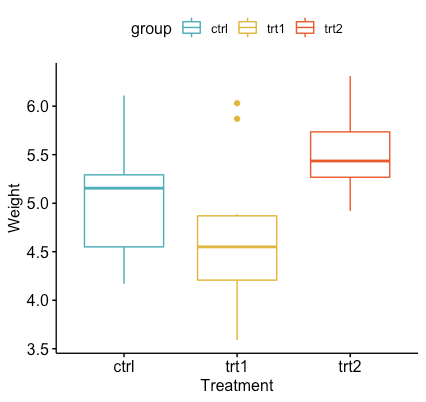
ggboxplot(my_data, x = "group", y = "weight", 
          color = "group", palette = c("#00AFBB", "#E7B800", "#FC4E07"),
          order = c("ctrl", "trt1", "trt2"),
          ylab = "Weight", xlab = "Treatment")

# Mean plots
# ++++++++++++++++++++
# Plot weight by group
# Add error bars: mean_se
# (other values include: mean_sd, mean_ci, median_iqr, ....)
library("ggpubr")
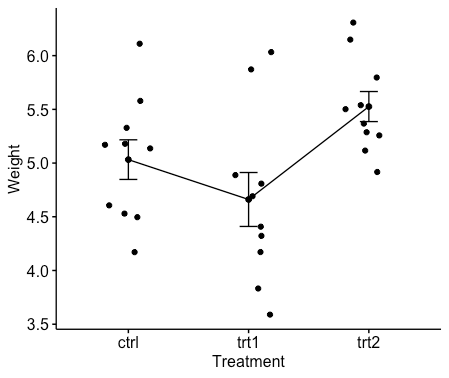
ggline(my_data, x = "group", y = "weight", 
       add = c("mean_se", "jitter"), 
       order = c("ctrl", "trt1", "trt2"),
       ylab = "Weight", xlab = "Treatment")

 # Box plot
boxplot(weight ~ group, data = my_data,
        xlab = "Treatment", ylab = "Weight",
        frame = FALSE, col = c("#00AFBB", "#E7B800", "#FC4E07"))
# plotmeans
library("gplots")
plotmeans(weight ~ group, data = my_data, frame = FALSE,
          xlab = "Treatment", ylab = "Weight",
          main="Mean Plot with 95% CI") 
          
# Compute the analysis of variance
res.aov <- aov(weight ~ group, data = my_data)

# Summary of the analysis
summary(res.aov)

# In one-way ANOVA test, a significant p-value indicates that some of the group means are different, 
# but we don’t know which pairs of groups are different.
TukeyHSD(res.aov)                                    

进阶

HSD

general linear hypothesis tests

repalce by Pairewise t-test under BH adjust

test validity

One-Way vs Two-Way ANOVA: Differences, Assumptions and Hypotheses