参考:
Suffix array - Wiki
6.3 Suffix Arrays - 算法红宝书
基本概念
应用:字符串处理、生物信息序列处理
后缀:学过英语的都知道什么叫后缀,就是从某个位置开始到字符串结尾的特殊子串,记住 Suffix(i)=S[i...len(S)-1],i就是后缀起始位置
后缀数组:就是将后缀排序好后放到一个一维数组里,SA[i]存放排名第i大的后缀首字符下标,并且保证 Suffix(SA[i])<Suffix(SA[i+1]), 1<=i<n 。
Rank数组:rank[i]存放suffix(i)的优先级
注:后缀数组和Rank数组为互逆运算。我们只要算出了sa数组,就可以在O(n)的时间复杂度内算出rank数组。
height数组:height[i]保存的是suffix(i)和suffix(i-1)的最长公共前缀的长度。也就是排名相邻的两个后缀的最长公共前缀。
看图说话:
下面列出了aabaaaab的所有后缀,并对其标号1..8

构造Rank数组,对每个i一次计算其后缀的排名,如下第一个后缀排名第4,所以Rank数组第一个为4
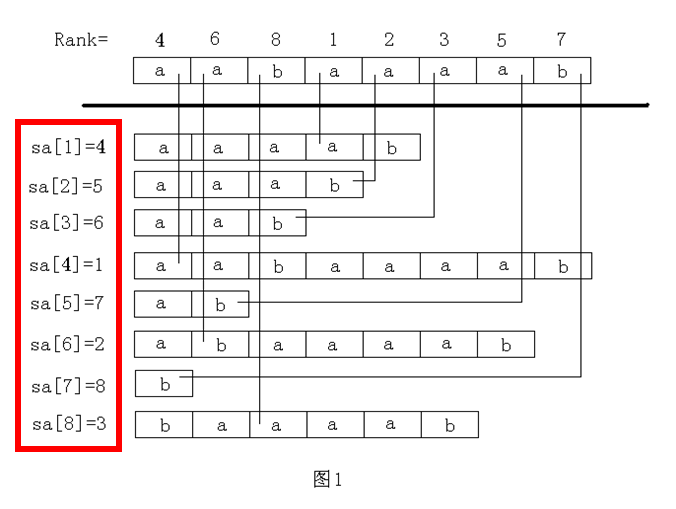
怎么构造后缀数组
构造sa数组
构造rank数组
构造height数组
例子
aabaaaab
aabaaaab
总共有n=8个后缀:
1: aabaaaab 2: abaaaab 3: baaaab 4: aaaab 5: aaab 6: aab 7: ab 8: b
按照字典序排序后
sa[ 1 ] = 4 aaaab sa[ 2 ] = 5 aaab sa[ 3 ] = 6 aab sa[ 4 ] = 1 aabaaaab sa[ 5 ] = 7 ab sa[ 6 ] = 2 abaaaab sa[ 7 ] = 8 b sa[ 8 ] = 3 baaaab
rank数组为:
rank[1]=4 rank[2]=6 rank[3]=8 rank[4]=1 rank[5]=2 rank[6]=3 rank[7]=5 rank[8]=7
height数组为:
height[ 1 ]=null height[ 2 ]= 3 height[ 3 ]= 2 height[ 4 ]= 3 height[ 5 ]= 1 height[ 6 ]= 2 height[ 7 ]= 0 height[ 8 ]= 1
因此,所有子串的最长公共子串就是3.