图之BFS和DFS遍历的实现并解决一次旅游中发现的问题

这篇文章用来复习使用BFS(Breadth First Search)和DFS(Depth First Search) 并解决一个在旅游时遇到的问题.

关于图的邻接表存储与邻接矩阵的存储,各有优缺点.但是邻接矩阵继承了数组的优点--在索引方面速度相比链表要快的多.由于以前我实现过邻接矩阵的存储方式,这次就用邻接表的方式复习吧.

图的邻接表存储简单示意

---

0.前提

• 类中的api以及属性

class CGraph
{
public:
	CGraph(void);
	~CGraph(void);
	// 根据顶点的数量初始化邻接表.
	void initVertex(int _vertexNum);
	// 添加一条边至图中.
	int addEdge(edge_s _edge);
	// 使用bfs遍历
	void traversal_bfs(int _vertex);
	// 使用dfs遍历
	void traversal_dfs(int _vertex);
	// 显示图的基本存储信息
	void printGraphVertex();
private:
	// 顶点数量
	int vertexNum;
	// 边数量
	int edgeNum;
	// 顶点数组
	Node_s * vertexPtr;
	// 记录顶点被访问状态
	VISITEDSTATE * visited;
private:
	// 更新访问状态
	void updateVisited();
	// 用于dfs遍历
	void dfs(int _vertex);
	// 改变顶点被访问状态
	void setVertexState(int _vertex,VISITEDSTATE _state);
	// 获取顶点被访问状态
	VISITEDSTATE getVertexState(int _vertex);
};

• 节点的定义与其初始化

enum VISITEDSTATE{
	VISITED = 0, 
	NOVISIT = 1
};
// 顶点的定义
struct Node_s {
	Node_s():verIndex(0),weight(0),NEXT(nullptr){}
    // 顶点的编号
	int verIndex;
    // 权重
	int weight;
	Node_s * NEXT;
};
// 边的定义
struct edge_s {
	edge_s() :start(0),end(0),weight(0){}
	int start;
	int end;
	int weight;
};
//节点的初始化,edgeNum是边的数量.
void CGraph::initVertex(int _vertexNum){
	vertexNum	= _vertexNum;
	edgeNum = 0;
	vertexPtr = new Node_s[vertexNum]();
    // // 记录顶点被访问状态的数组
	visited = new VISITEDSTATE[vertexNum]();
	for (int i = 0;i < vertexNum;i++) 
	{
		visited[i]	= NOVISIT;
		vertexPtr[i].verIndex = i;
		vertexPtr[i].weight = 0;
		vertexPtr[i].NEXT	= nullptr;
	}
}

• 边的加入(图的构建)

int CGraph::addEdge(edge_s _edge){
	int start	= _edge.start;
	int end	= _edge.end;
	if (start >= vertexNum || end >= vertexNum)
	{
		std::cout <<"此顶点不存在于邻接表中"<<std::endl;
		return -1;
	}
	Node_s * new_node = new Node_s;
	if (!new_node) 
	{
		return -1;
	}
	// 头插入法
	new_node->verIndex	= end;
	new_node->weight	= _edge.weight;
	new_node->NEXT		= vertexPtr[start].NEXT;
	vertexPtr[start].NEXT = new_node;

	edgeNum ++;
	return 0;
}

1.BFS

　　非常类似于树的层序遍历

void CGraph::traversal_bfs(int _vertex){
	updateVisited();
	std::queue<Node_s *> vertexQ;
	setVertexState(_vertex,VISITED);

	vertexQ.push(&vertexPtr[_vertex]);
	while (!vertexQ.empty())
	{
		Node_s * vertex_pop = vertexQ.front();
		vertexQ.pop();
		std::cout << vertex_pop->verIndex<<" ";
		
		Node_s * node = vertex_pop->NEXT;
		while (node)
		{
			if (getVertexState(node->verIndex) == NOVISIT)
			{
				setVertexState(node->verIndex,VISITED);
				vertexQ.push(&vertexPtr[node->verIndex]);
			}
			node = node->NEXT;
		}
	}
	std::cout <<std::endl;
}

2.DFS

　　DFS的实现需要至少需要两个函数,一个负责调用,一个负责递归.

void CGraph::traversal_dfs(int _vertex){
	updateVisited();
	dfs(_vertex);
	std::cout <<std::endl;
}

负责递归的dfs函数:

void CGraph::dfs(int _vertex){
	std::cout << _vertex <<" ";
	setVertexState(_vertex,VISITED);

	for (Node_s * node = vertexPtr[_vertex].NEXT;node;node=node->NEXT) 
	{
		if (getVertexState(node->verIndex) == NOVISIT)
		{
			dfs(node->verIndex);
		}
	}
}

%DFS示意

3.在旅游时遇到的一个小问题

假期去张家界天门山旅游,走了一大圈发现还挺大;
就寻思着能不能找到一条路把全部景点都走完.这个图论中有讲过啊!!
问题抽象如下:


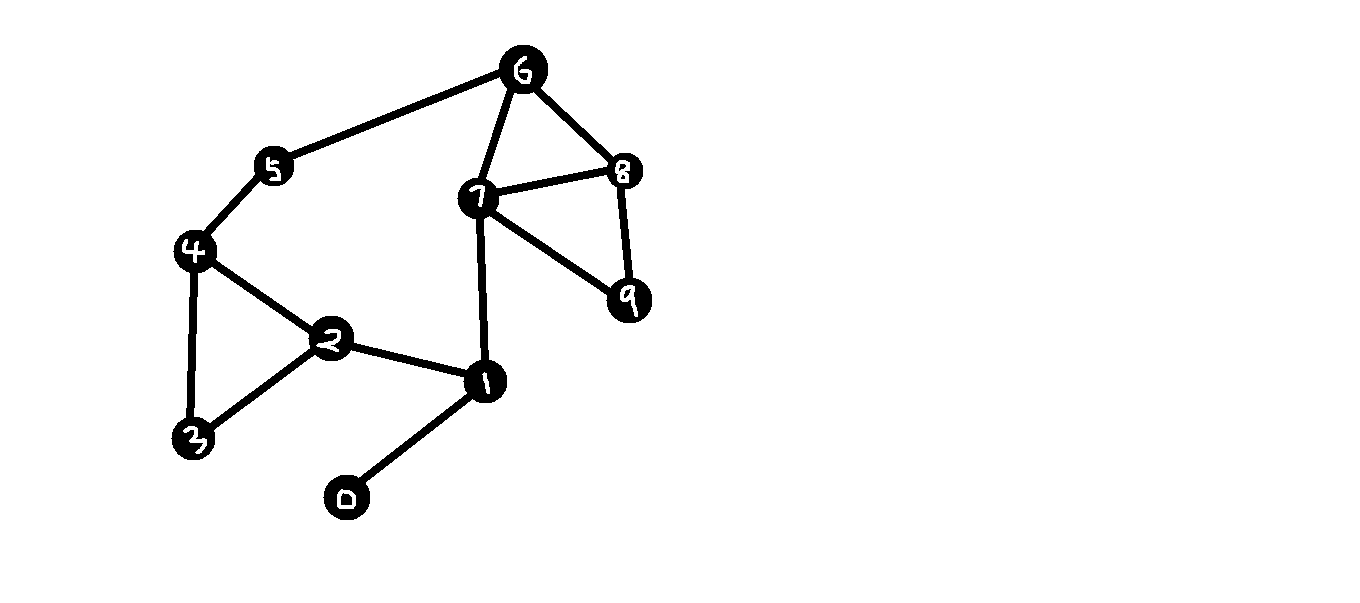
我把图中的点转化为图,并进行编号.
(左下角的那个点为0,由虚线连接的那个为9),共十个点
然后按照　顶点数 + "起始点-终点-权值"　的格式写入文件: 权值暂时没意义 (也不是,见后文)
10
0 1 50
1 0 50
1 2 50
...
8 9 50
9 8 50
9 7 50

其实最终要的线路要求如下:

• 起点是0, 只能从0上山
• 终点是9 , 因为只有9才能下山
• 需要走过的顶点数尽可能多

利用回溯,DFS上场:

// 一条线路的定义
struct path_s{
	path_s():totalWeight(0),vertexVec(){}
	// 顶点集合
	std::vector<int> vertexVec;
	// 总的权值
	WEIGHTYPE totalWeight;
};

void CGraph::throughPathLongest(int _vertex){
	path_s path;
	dfs_path(path , _vertex);
}

void CGraph::dfs_path(path_s & _vertexPath,int _vertex){
	_vertexPath.vertexVec.push_back(_vertex);
	setVertexState(_vertex, VISITED);
	// 存储把当前路线
	addTolongestPath(_vertexPath);

	for (Node_s * head = vertexPtr[_vertex].NEXT;head;head=head->NEXT) 
	{
		if (getVertexState(node->verIndex) == NOVISIT)
		{
			_vertexPath.totalWeight += head->weight;
			dfs_path(_vertexPath,head->data);
			// 回溯,处理当前节点
			_vertexPath.totalWeight -= head->weight;
			_vertexPath.vertexVec.pop_back();

			setVertexState(_vertex, NOVISIT);
		}
	}
}

// 根据加入线路的规则,具体实现如下
int CGraph::addTolongestPath(path_s &_vertexPath){
	// 若路径为空,则直接设置为当前路径
	if (pathVec.empty())
	{
		pathVec.push_back(_vertexPath);
	}
	else
	{
		// 终点是9,而且要大于已经存储的线路所含节点数
		if (_vertexPath.vertexVec.back() == 9 && 
			_vertexPath.vertexVec.size() > pathVec.back().vertexVec.size())
		{
			pathVec.clear();
			pathVec.push_back( _vertexPath);
		}
		else
        	// 否则只是一条含有相同目的地所经过顶点不同的线路而已.
			if (
				_vertexPath.vertexVec.back() == 9 &&
				_vertexPath.vertexVec.size() == pathVec.back().vertexVec.size())
			{
				pathVec.push_back(_vertexPath);
			}
	}
}

最后显示一下pathVec中的结果即可:
结果显示如下:
NO.0:
0->1->2->3->4->5->6->7->9 (400)
NO.1:
0->1->2->3->4->5->6->8->9 (400)

哈哈,我们选择的是NO.1的线路,因为那边有风景看.(其实之前我们坐到7又返回了...

相关代码见我的github
里面有让你走完全部景点的路径,不过终点不是9 ,这意味着我逛完后还要重复的线路到9:(
突然觉得景点有点鸡贼 (逃

总结:

• BFS就是一个函数,而且没有显示的使用堆栈,这对大数据的遍历很有利;
• DFS对于寻找要求的路径很有好处,但是递归太深是个需要考虑的地方;
• 出去旅游有必要先写一个程序判断能够看完所有景点的最佳路径:)