数据结构和算法
1：程序设计=数据结构+算法。
数据结构就是关系，就是数据元素之间的一个或多种特定关系。
数据结构：1）逻辑结构（集合结构，线性结构，树形结构，图形结构），2）物理结构（数据存储方式，顺序存储，链式存储）。
2：算法：解决特定问题求解步骤的描述，计算机中表现为多个指令的有限序列，并且每条指令表示一个或多个操作。
算法的特性：输入（0个或多个），输出（至少一个），有穷（有限步内完成），确定（无歧义），可行（每一步都是可行的）。
3：算法效率的度量方法：效率或执行时间。
影响因素：1）算法策略；2）编译产生的代码质量；3）问题的输入规模；4）机器的指令执行速度；
判断效率时，关注最高项即可（忽略次要项以及系数）。
4：时间复杂度和空间复杂度：O（），又称大O记法。一般情况下，随着输入规模n的增大，T（n）增长最慢的算法为最优算法。0(1)<0(logn)<O(n)<0(nlogn)<0(n^2)<0(n^3)<0(2^n)<0(n!)<0(n^n),
时间复杂度表示运行时间的需求，空间复杂度表示空间需求。
5：线性表：零个或多个元素组成的有限序列。（第一个无前驱，最后一个无后继，其余元素都有一个前驱和后继。元素的个数为n。）
数据类型：是指一组性质相同的值的集合及定义在此集合上的一些操作的总称。例如，编程语言中的整型，浮点型等。
抽象数据类型ADT：对数据类型进行抽象，抽取出事务具有的普遍性的本质，是特征的概括，而不是细节。（数据类型和相关的操作捆绑在一起）
线性表抽象数据类型（List）:
Data:线性表的数据对象集合为{a,b,c...},每一个元素的数据类型为DataType
Operation: InitList(*L),初始化，判断，取值，返回，插入...
6：线性表的顺序存储结构：类似于数组，元素依次排放。顺序结构封装的三个属性：数据起始地址，线性表最大长度，当前线性表长度。线性表是从1开始，而数组是从0开始。
插入和删除：首先判断插入删除的位置是否合理，然后插入是从插入位置开始向后移动一位，完成后插入元素，删除则是去除需要删除的元素，然后后面的元素开始依次向前移动一位。
线性表的读取为0(1)，插入和删除都是0（n）.
优点：无需为表示表中的元素之间的逻辑关系而增加额外的存储空间，可以快速的存取表中的任意位置的元素。
缺点：插入和删除时需要移动大量元素，当线性表长度变化较大时，难以确定存储空间的容量。
7:线性表的链式存储结构：每个元素多用一个位置来存放指向下一个元素位置的指针，依次类推，可以找到所有的元素。现在的链式存储中，除了要存储数据本身外，还要存储它的后继元素的存储地址（指针）。
数据域：存储数据信息的域；指针域：存储直接后继位置的域。这两部分信息组成数据元素称之为存储映像，节点Node。
链表中每个结点中只包含一个指针域，为单链表。链表中的第一个界点的存储位置叫做头指针，最后一个界点指针为空。
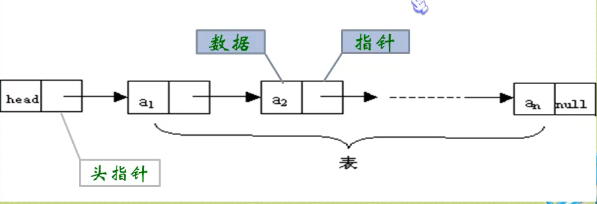
8：头节点和和头指针：头节点一般不存储任何数据信息。
头指针：
头指针是指链表指向第一个结点的指针，若链表有头节点，则是指向头结点的指针。
头指针具有标识作用，常用头指针冠以链表的名字（指针变量的名字）。
无论链表是否为空，头指针均不为空。
头指针是链表的必要元素。
头节点：
放在第一个元素的结点之前，其数据域一般无意义（可以用来存放链表长度），是为了操作的统一方便设立（在第一元素结点前插入和删除第一结点与其他结点操作统一）。
头节点不一定是链表的必要元素。
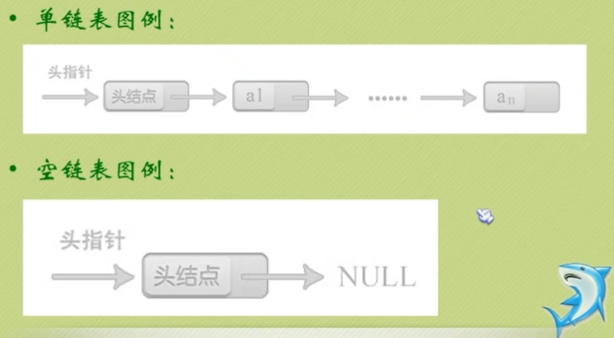
单链表的读取？在线性表顺序存储结构中，计算任意一个元素的存储位置是很容易的，但在单链表结构中，第i个元素的如何获取？--》工作指针后移。
9：单链表的插入：
只需要更改ai和s节点的指针域：应该首先更改结点s的指针域！
s->next=p->next;
p->next=s;
code：
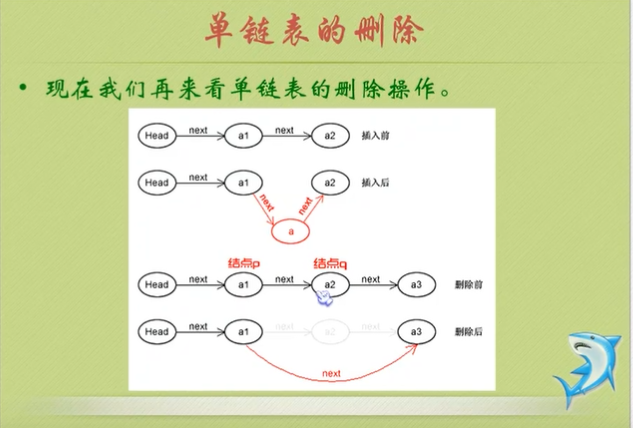
p->next=p->next->next;或q=p->next; p->next=q->next;
对于插入或删除数据越频繁的操作，单链表的效率优势越明显。
10：单链表的整表创建
顺序存储结构的线性表可以类比于数组的初始化，单链表的数据分散在内存在各个角落。创建单链表是一个动态生成链表的过程。
头插法：从一个空表开始，生成新节点，读取的数据放到新节点的数据域中，然后将新节点插入到当前链表的表头上。也就是说，把新加的元素放在表头后的第一个位置。
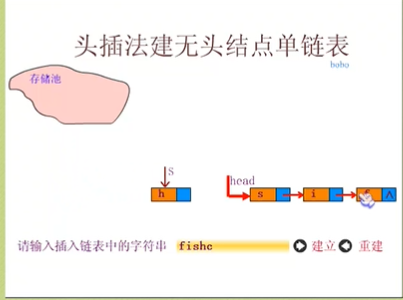
头插法表中的元素顺序是与原来相反的。
尾插法：把新节点插入链表的最后，需要增加一个指向链表最后一个尾节点的指针r。
r->next=p;
r=p;
11：单链表的整表删除
声明结点p和q；
将第一个结点赋给p，下一节点赋值给q；
循环执行释放p和将q赋值给p的操作；
1 LinkList p,q; 2 p= (*L)->next; 3 while(p) 4 { 5 q=p->next; 6 free(p); 7 p=q; 8 } 9 (*L)->next=Null; 10 return OK;
单链表结构与顺序存储结构的优缺点：
| 优缺点 | 顺序存储结构 | 单链表 |
| 存储分配方式： | 一段连续的存储单元依次存储线性表的数据元素 | 链式存储，用一组任意的存储单元存放线性表的元素 |
| 时间性能： | 查找O(1)，插入和删除O(n) | 查找O(n)，插入和删除O(1) |
| 空间性能： | 需要预先分配存储空间，较大浪费，较小溢出 | 利用零碎空间 |
若线性表需要频繁查找，很少进行插入和删除操作，采用顺序存储结构合适。 例如用户注册信息，绝大多数都是读取数据。
若需要频繁的插入和删除，采用单链表合适。
12：静态链表
C语言的魅力在于指针的灵活性，使得它可以非常容易的操作内存中的地址和数据，比其他高级语言更加的灵活方便。（面向对象使用对象引用机制间接的实现了指针的某些功能。）
用数组描述的链表称为静态链表。有两队元素：下标和游标。游标指向下一个元素的下标。游标类似于链表中的地址指针。数组的第一个和最后一个元素不存放数据，数组第一个游标存放数组第一个非空元素的下标，数组最后一个游标存放数组的第一个非空元素的下标。数组元素的最后一个非空元素的游标为0.同时，静态链表中的内存的获取与释放需要编程实现。
13：循环链表
单链表只是单向的，如果不从头结点出发，就无法访问到全部结点。
将单链表中终端结点的指针端由空指针改为指向头节点，形成一个环，这种头尾相接的单链表为单循环链表。
14：不用头指针，使用尾指针指向最后一个。
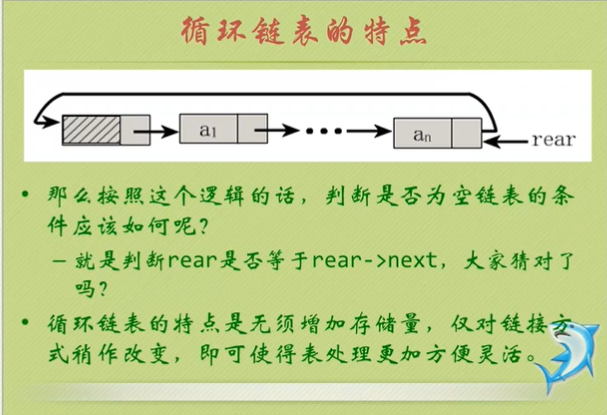
判断单链表是否有环？
双向链表
双向链表的插入操作：(注意顺序)
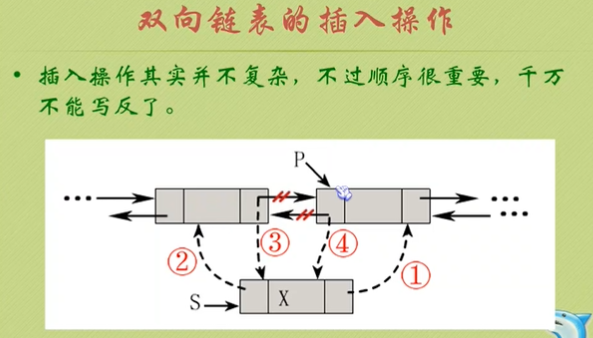
s->next=p; s->prior=p->prior; p->prior->next=s; p->prior=s;
删除结点：
p->prior->next=p->next; p->next->prior=p->prior; free(p);
双向链表可以有效的提高算法的时间性能，用空间换取时间。
#include <stdio.h> #include <stdlib.h> #define OK 1 #define ERROR 0 typedef char ElemType; typedef int Status; typedef struct DualNode { ElemType data; struct DualNode* prior; struct DualNode* next; }DualNode, *DuLinkList; Status InitList(DuLinkList *L) { DualNode *p, *q; int i; *L = (DuLinkList)malloc(sizeof(DualNode)); if (!(*L)) { return ERROR; } (*L)->prior = (*L)->next = NULL; p = (*L); for (i = 0; i < 26; i++) { q = (DualNode*)malloc(sizeof(DualNode)); if (!q) { return ERROR; } q->data = 'A' + i; q->prior = p; q->next = p->next; p->next = q; p = q; } p->next = (*L)->next; (*L)->next->prior = p; (*L)->prior = p->prior; return OK; } void Caesar(DuLinkList* L, int i) { if (i > 0) { do { (*L) = (*L)->next; } while (--i); } if (i < 0) { do { (*L) = (*L)->prior; } while (++i); } } int main() { DuLinkList L; int i,n; InitList(&L); printf("请输入一个整数："); scanf_s("%d", &n); printf(" "); Caesar(&L, n); for (i = 0; i < 26; i++) { L = L->next; printf("%c", (L)->data); } printf(" "); return 0; }
15：栈（Stack）和队列
栈是一个后进先出的线性表，它要求只在表尾进行删除和插入操作。
所谓的栈，其实就是一个特殊的线性表。表尾称为栈顶（Top），相应的表头称为栈底（Bottom）。
栈的插入（Push）,栈的删除（Pop）.最开始栈中不包含任何数据，称为空栈，此时栈顶就是栈底，然后数据从栈顶进入，栈顶和栈底分离。数据出栈时从栈顶弹出，栈顶下移，整个栈的当前容量变小。
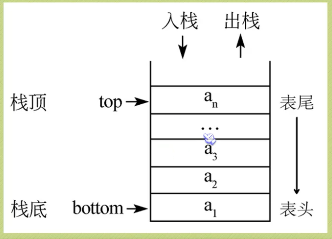
入栈操作在栈顶进行，每次向栈中压入一个数据，top指针加1，直到栈满为止。
出栈操作就是在栈顶取出数据，栈顶指针下移，栈的当前容量-1。
逆波兰表达式：（没有括号）逆波兰表达式又叫做后缀表达式，是一种没有括号，并严格遵循“从左到右”运算的后缀式表达方法。
它的优势在于只用两种简单操作，入栈和出栈就可以搞定任何普通表达式的运算。其运算方式如下：
创建一个队列：首先在内存中创建一个头节点，然后将队列的头指针和尾指针都指向这个生成的头结点，此时为空队列。
队列的顺序存储结构：假设一个队列有n个元素，则顺序存储的队列需要建立一个大于n的存储单元，并把队列的所有元素存储在数组的前n个单元，数组下标为0的一端是队头。
如果队头指针可以移动，那么出队列复杂度就可以下降。但要解决假溢出的问题。循环队列,取模操作。
17：递归和分治思想：（归去来兮，递归效率较低，能用迭代最好用迭代，递归是函数自己调用自身，每次调用都需要入栈等操作。）
斐波那契数列的递归序列：
#include <stdio.h> int Fib(int i); int main() { int i; printf_s("请输入一个大于零的整数 "); scanf_s("%d", &i); for (; i >= 0; i--) { printf_s("%d ", Fib(i)); } return 0; } int Fib(int i) { if (i < 2) return i == 0 ? 0 : 1; return Fib(i - 1) + Fib(i - 2); }
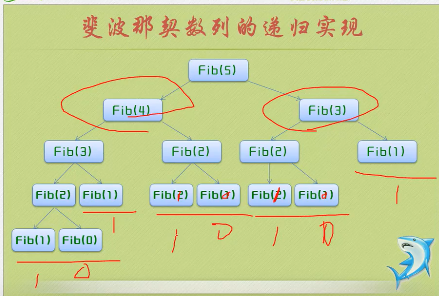
递归定义至少有一个终止条件，函数不再调用自身，开始返回。
递归和迭代的区别：迭代使用的是循环结构，递归使用的是选择结构。但大量的递归调用会建立函数的副本，会消耗大量的时间和内存，而迭代不需要这种付出。
递归函数分为调用阶段和回退阶段，递归的回退顺序是它调用顺序的逆序。
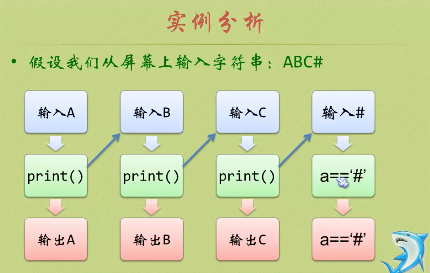是否可以理解为不断的中断，保存后不断调用自身，然后返回执行剩余。
void print() { char a; scanf_s("%c", &a); if (a != '#') print(); if (a != '#') printf_s("%c", a); }
分治思想：采取各个击破，分而治之的原则。当一个问题规模较大且不容易求解时，可以考虑将其分为几个小的模块，逐一解决。采用分治思想处理问题时，其各个小模块通常具有与大问题相同的结构。
八皇后问题回溯，也可以当作递归问题。
18：字符串："BoyFriend"，"KMP"
字符串String：是由零个或多个字符串组成的有限序列。
19：树（Tree）：是n(n>0)个结点的有限集。当n=0时，称为空树，在任意一个非空树当中：
1）有且仅有一个特定的称为根节点（Root）的结点；当n>1时，其余结点可以分为m(m>0)个互不相交的有限集T1,T2...,Tm,其中每一个集合本身又是一个树，并且称为根的子树（SubTree）。
n=0,根节点是唯一的。不能交叉。
2）结点拥有的子树数称为结点的度（Degree），树的度取决于树内各结点度的最大值。
3）度为0 的结点称为叶节点（Leaf）或终端结点；度不为0 的结点称为分支结点或非终端结点，除跟结点外，分支结点也称为内部结点。
4）结点的层次（Level）从根开始，根为第一层，根的孩子为第二层。树中结点的最大层次称为树的深度（Depth）或高度。
5）如果将树中结点的各子树看成从左到右，是有次序的，不能交换，则称该树为有序树，否则为无序树。
6）森林（Forest）是m(m>0)棵互不相交的树的集合。对树中的每个结点而言，其子树的集合即为森林。
20：树的存储结构
双亲表示法：假设以一组连续空间存储树的结点，同时在每个结点中，附设一个指示其双亲结点在数组中位置的元素。每个结点除了知道自己之外，还知道双亲结点的位置。
孩子表示法：
孩子双亲表示法：
21：二叉树（Binary Tree）
是n（n>=0）个结点的有限集合，该集合或者为空集（空二叉树），或者由一个根节点和两棵互不相交的，分别称为根节点的左子树和右子树的二叉树组成。