一、定义:
树(Tree):是n (n>0)个结点的有限集。
当n=0时 (根节点是唯一的),称为空树,在任意一个非空树当中:有且仅有一个特定的称为根节点(Root)的结点;当n>1时,其余结点可以分为m(m>0)个互不相交的有限集T1,T2...,Tm,其中每一个集合本身又是一个树,并且称为根的子树(SubTree)。
二、结点的分类:
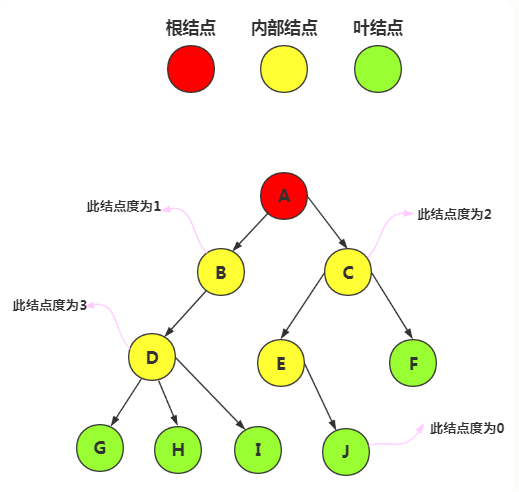
度(Degree):每个结点都有一个度,结点拥有的子树数称为结点的度(Degree),树的度取决于树内各结点度的最大值。
叶节点(Leaf)/叶子结点/ 终端结点:度为0 的结点。
分支结点/ 非终端结点:度不为0 的结点。
内部结点:除跟结点外的分支结点。
三、结点之间的关系
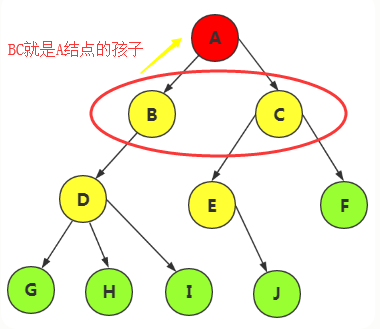
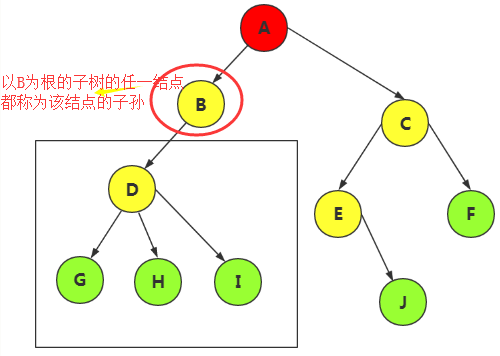
结点的子树的根称为该结点的孩子,(例如A结点的孩子为B,C)
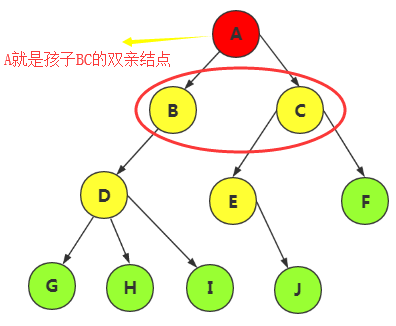
相反的,该结点称为孩子的双亲结点。(A称为B,C的双亲结点)
同一个双亲的孩子之间互称为兄弟

结点的祖先,从根到该结点所经分支上的所有结点
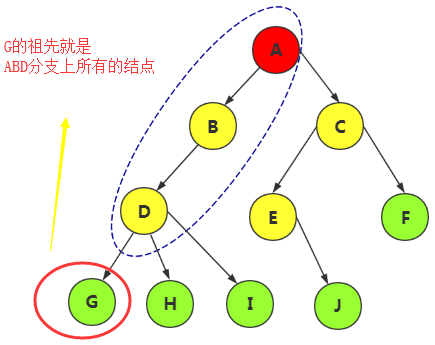
以某结点为根的子树中的任一结点都为该结点的子孙
四、树的层次
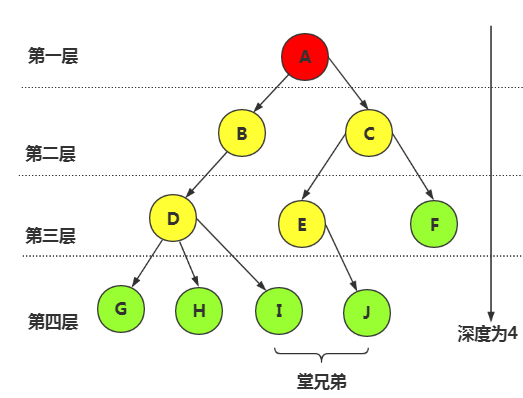
结点的层次(Level)从根开始,根为第一层,根的孩子为第二层。
双亲在同一层的结点互为堂兄弟。
树中结点的最大层次称为树的深度(Depth)或高度。
五、有序树和无序树
如果将树中结点的各子树看成从左到右,是有次序的,不能交换,则称该树为有序树,否则为无序树。
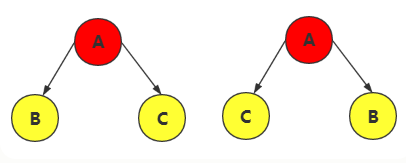
若两者表示同一颗树,就叫无序树
若两者表示2颗不同树,就叫做有序树
六、森林
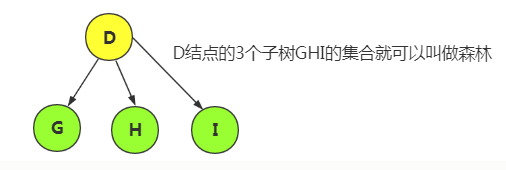
森林(Forest)是m(m>0)棵互不相交的树的集合。对树中的每个结点而言,其子树的集合即为森林。
七、和线性表的区别
1、线性表:
第一个数据元素:无前驱
最后一个数据元素:无后继
中间元素:一个前驱一个后继
2、树:
根结点:无双亲,唯一
中间结点:一个双亲,可以多个孩子
叶结点:无孩子,一棵树可以有多个叶结点
八、总结树的抽象数据类型
ADT 树(tree) Data 树是由一个根节点和若干棵子树构成。树中结点具有相同数据类型及层次关系 Operation InitTree(*T):构造空树T DestroyTree(*T):销毁树T CreateTree(*T,definition):按照definition中给出树的定义来构造树 ClearTree(*T):若树存在,则清空树 TreeEmpty(T):若树为空,返回true,否则false TreeDepth(T):返回树的深度 Root(T):返回T的根节点 Value(T,cur_e):cur_e是树T中的一个结点,返回此结点的值 Assign(T,cur_e,value):给树T的结点cur_e赋值为value Parent(T,cur_e):若cur_e是树的非根节点,则返回他的双亲,否则为空 LeftChild(T,cur_e):若cur_e是树的非叶结点,则返回他的最左结点,否则返回空 RightSibling(T,cur_e):若cur_e有右兄弟,则返回他的有兄弟,否则为空 InsertChild(*T,*p,i,c):插入一个树C到树T中,插入位置为p所指向的结点的第i个子树。记得将该结点的度加1 DeleteChild(*T,*p,i):删除树T中p所指向结点的第i棵子树 endADT