递归和分治思想（折半查找）

1、递归：（归去来兮）

递归效率较低，如果明确知道迭代次数，则能用迭代最好用迭代，递归是函数自己调用自身，每次调用都需要入栈等操作。但是递归操作要比迭代简单和清楚。

递归函数的优点是定义简单，逻辑清晰。理论上，所有的递归函数都可以写成循环的方式，但循环的逻辑不如递归清晰。

使用递归函数需要注意防止栈溢出。在计算机中，函数调用是通过栈（stack）这种数据结构实现的，每当进入一个函数调用，栈就会加一层栈帧，每当函数返回，栈就会减一层栈帧。由于栈的大小不是无限的，所以，递归调用的次数过多，会导致栈溢出。

解决递归调用栈溢出的方法是通过尾递归优化，事实上尾递归和循环的效果是一样的，所以，把循环看成是一种特殊的尾递归函数也是可以的。

尾递归是指，在函数返回的时候，调用自身本身，并且，return语句不能包含表达式。这样，编译器或者解释器就可以把尾递归做优化，使递归本身无论调用多少次，都只占用一个栈帧，不会出现栈溢出的情况。

尾递归调用时，如果做了优化，栈不会增长，因此，无论多少次调用也不会导致栈溢出。

遗憾的是，大多数编程语言没有针对尾递归做优化。

递归需要遵守的重要规则：

1）执行一个方法时，就创建一个新的受保护的独立空间（栈空间）；

2）方法的局部变量是独立的，不会相互影响；

3）如果方法中使用的是引用类型变量（比如数组），就会共享该引用类型的数据；

4）递归必须向退出递归的条件逼近，否则就会是无限递归（导致栈溢出）；

5）当一个方法执行完毕，或者遇到return，就会返回，遵守谁调用，就将结果返回给谁，同时当方法执行完毕或者返回时，该方法也就执行完毕。

递归用于解决什么样的问题：

1）各种数学问题：8皇后问题，汉诺塔，阶乘问题，迷宫问题，球和篮子问题等；（回溯，如果不能则会返回继续寻找）

2）各种算法中，例如快速排序，归并排序，二分查找，分治算法等；

3）将用栈解决的问题，利用递归代码会更加简洁。

2、斐波那契数列的递归实现

#include <stdio.h>
int Fib(int i);
int main()
{
    int i;
    printf_s("请输入一个大于零的整数
");
    scanf_s("%d", &i);
    for (; i >= 0; i--)
    {
        printf_s("%d ", Fib(i));
    }
    
    return 0;
}

int Fib(int i)
{
    if (i < 2)
        return i == 0 ? 0 : 1;
    return Fib(i - 1) + Fib(i - 2);
}

1）递归定义至少有一个终止条件，函数不再调用自身，开始返回。

2）递归和迭代的区别：迭代使用的是循环结构，递归使用的是选择结构。但大量的递归调用会建立函数的副本，会消耗大量的时间和内存，而迭代不需要这种付出。

3）递归函数分为调用阶段和回退阶段，递归的回退顺序是它调用顺序的逆序。

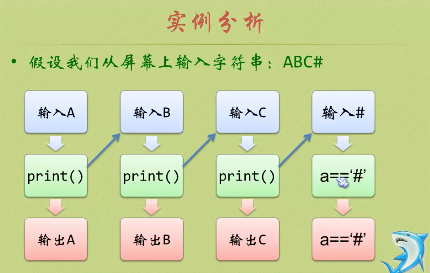
举例：打印输入字符的倒序输出：

void print()
{
    char a;
    scanf_s("%c", &a);
    if (a != '#') print();
    if (a != '#') printf_s("%c", a);
}

3、分治思想

采取各个击破，分而治之的原则。当一个问题规模较大且不容易求解时，可以考虑将其分为几个小的模块，逐一解决。采用分治思想处理问题时，其各个小模块通常具有与大问题相同的结构。

4、折半查找

折半查找法，是一种常用的查找方法，该方法通过不断缩小一半查找的范围，直到达到目的，所以效率比较高

前提：针对有序数组（元素从小到大或从大到小），优点是查找速度比较快，时间复杂度为O(log₂n)。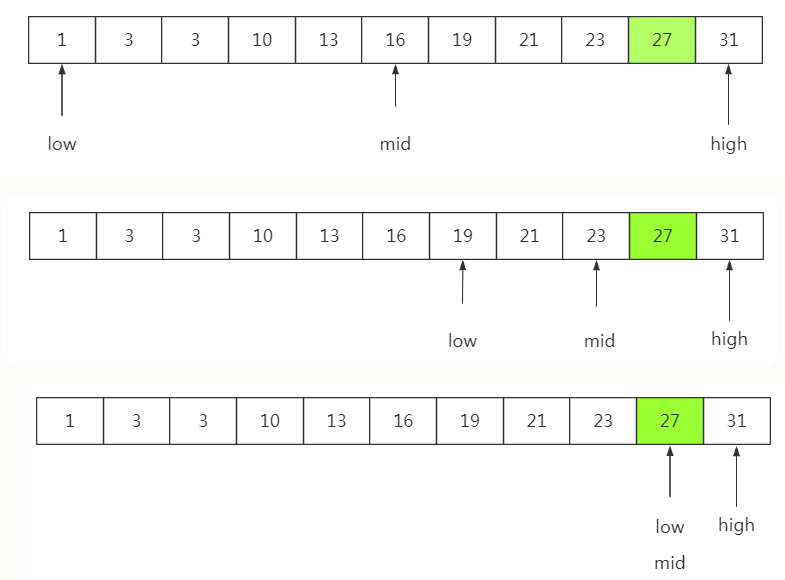

 迭代实现：

int main()
{
    int a[11] = { 1, 3, 3, 10, 13, 16, 19, 21, 23, 27, 31 };
    int left, mid, right,num;
    left = 0;
    right = 10;
    num = 27;

    while (left <= right)
    {
        mid = (left + right) / 2;
        if (a[mid] > num)
            right = mid - 1;
        else if (a[mid] < num)
            left = mid + 1;
        else
            break;
    }
    printf("index:%d", mid);
    system("pause");
    return 0;
}

递归实现

int binary_search(int arr[], int left, int right,int ele)
{
    int mid = (left + right) / 2;  //边界条件是找到当前值，或者查找范围为空。否则每一次查找都将范围缩小一半。
　　 if(left>right)
　　 {
　　　　　return -1;　　
    }
　　else
{
　　if (arr[mid] > ele)
        right = mid - 1;
    else if (arr[mid] < ele)
        left = mid + 1;
    else
        return mid;
    return binary_search(arr, left, right, ele);
}
}

int main()
{
    int a[11] = { 1, 3, 3, 10, 13, 16, 19, 21, 23, 27, 31 };
    int left, right, num, index;
    left = 0;
    right = 10;
    num = 27;

    index = binary_search(a, left, right, num);
    
    printf("index:%d", index);
    system("pause");
    return 0;
}

上面讲的递归的二分查找法就是一个分治算法的典型例子，分治算法常常是一个方法，在这个方法中含有两个对自身的递归调用，分别对应于问题的两个部分。

二分查找中，将查找范围分成比查找值大的一部分和比查找值小的一部分，每次递归调用只会有一个部分执行。