1、二叉树(Binary Tree)
是n(n>=0)个结点的有限集合,该集合或者为空集(空二叉树),或者由一个根节点和两棵互不相交的,分别称为根节点的左子树和右子树的二叉树组成。
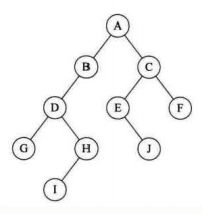
2、特数二叉树
1)斜二叉树
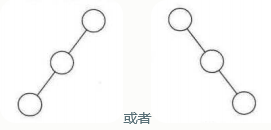
所有的结点都只有左子树的二叉树叫做左斜树
所有的结点都只有右子树的二叉树叫做右斜树
相当于链表,所以线性结构可以理解为是树的一种极其特殊的表现形式
2)满二叉树(完美二叉树)

所有分支结点都存在左子树和右子树。
所有叶子结点都在同一层
3)完全二叉树

对树按照上->下,左->右,编号为i的与满二叉树中为i的位置相同。
3、二叉树的重要性质
性质一:第i层最大结点数位2^(i-1)个,(i>=1)
性质二:深度为k的二叉树至多有2^k-1个结点
性质三:叶结点n0与度为2的结点n2的个数关系n0=n2+1
性质四:具有n个结点的完全二叉树的深度为[log2n]+1
性质五:对一棵有n个结点的完全二叉树,从第一层到最大层,对任一结点i(1=<i<=n)有:
注意:下标是从1开始的。
1.非根节点的父节点序号是[i/2]
2.结点(序号i)的左孩子为2i,若2i>n没有左孩子
3.结点(序号i)的右孩子为2i+1,若2i+1>n没有右孩子

但一般数组下标是从0开始的:
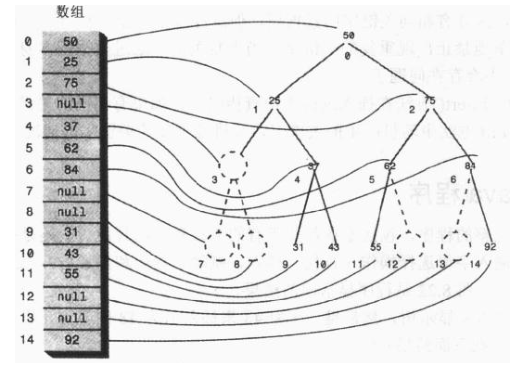
树中的每个位置,无论是否存在节点,都对应于数组中的一个位置,树中没有节点的在数组中用0或者null表示。
假设节点的索引值为index,那么节点的左子节点是 2*index+1,节点的右子节点是 2*index+2,它的父节点是 (index-1)/2。
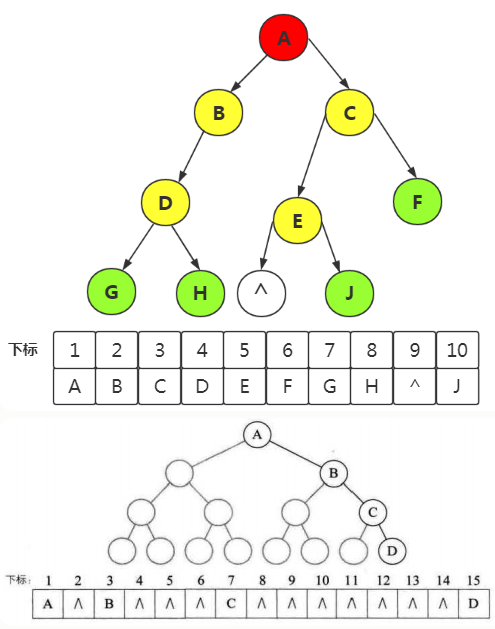
4、二叉树的顺序存储结构
一般树很难用数组存储,但完全二叉树可以,(从上->下,从左->右,层序遍历)。同时可以利用完全二叉树的性质5,快速获得结点的双亲与孩子位置。
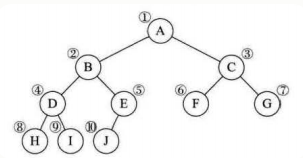

二叉树的顺序存储结构就是用一维数组存储二叉树中的结点,并且结点的存储位置,可以使用性质五来提现结点之间关系。这就是完全二叉树的优越性。
补充:对于一般二叉树也可以使用顺序存储(不过需要对空结点进行补全为^,变为一棵完全二叉树先)
我们需要结合数的结构来考虑,一棵普通的二叉树能否使用该方法。
如果是接近完全二叉树的二叉树,我们可以补全,
但是对于一棵类似于右斜二叉树,则完全没有必要,会大量浪费空间
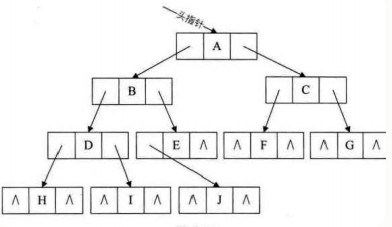
5、二叉链表

//二叉树的二叉链表结点结构定义 typedef struct BiTNode //结点结构 { TElemType data; //结点数据 struct BiTNode *lchild, *rchild; //左右孩子指针 }BiTNode,*BiTree;
6、二叉树的遍历(递归方式)
1)前序遍历(根左右,从根节点开始遍历)

void PreOrderTraversal(BinTree BT) { if (BT) { printf("%d", BT->data); PreOrderTraversal(BT->lchild); PreOrderTraversal(BT->rchild); } }
2)中序遍历(左根右,注意从最左侧叶子节点开始遍历)

void InOrderTraversal(BinTree BT) { if (BT) { InOrderTraversal(BT->lchild); printf("%d", BT->data); InOrderTraversal(BT->rchild); } }
3)后序遍历(左右根,依然从最左侧叶子节点开始)

void PostOrderTraversal(BinTree BT) { if (BT) { PostOrderTraversal(BT->lchild); PostOrderTraversal(BT->rchild); printf("%d", BT->data); } }
4)层序遍历(顺序存储)利用队列。
import java.util.*; /** public class TreeNode { int val = 0; TreeNode left = null; TreeNode right = null; public TreeNode(int val) { this.val = val; } } */ public class Solution { public ArrayList<Integer> PrintFromTopToBottom(TreeNode root) { Queue<TreeNode> queue=new LinkedList<>(); ArrayList<Integer> list=new ArrayList<Integer>(); if(root==null) return list; queue.offer(root); while(!queue.isEmpty()) { int size=queue.size(); for(int i=0;i<size;i++) { TreeNode node=queue.poll(); list.add(node.val); if(node.left!=null) queue.offer(node.left); if(node.right!=null) queue.offer(node.right); } } return list; } }
二叉树前、中、后三种遍历的非递归实现方式:

前序和后序遍历:前序遍历和后序遍历归为一类,所用思想基本一模一样:
前序遍历的步骤为 :
①对root进行异常处理
②将root压入栈
③while循环遍历,终止条件为栈为空,所有元素均已处理完
④从栈顶取元素读,取并存入结果
⑤将取出元素的右、左节点分别压入栈内,以便下次循环取元素时为本次节点的左,右子节点.
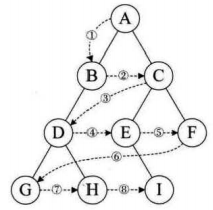
运用辅助栈,保存遍历到的节点(用栈后入先出的特性,控制已经遍历到的节点的访问顺序). 以前序深度优先遍历为例,先访问根节点,然后访问左树,左树全部访问完了,再访问右树
后续遍历思想: 左-右-根;可以视为, 根-右-左,然后结果转置即可. 如前面示意图,根右左,访问顺序则为:ACFBED;可以看出,这样访问刚好为后续遍历的转置. 根右左访问与前序(根左右)遍历操作思想一模一样
①前序遍历
/** * 前序遍历,迭代法 */ public List<Integer> preorderTraversal(TreeNode root) { List<Integer> result = new ArrayList<>(); if (root == null) return result; Stack<TreeNode> stack = new Stack<>(); stack.push(root); while (!stack.isEmpty()) { TreeNode node = stack.pop(); result.add(node.val); if (node.right != null) stack.push(node.right); //先压入右节点,后出栈 if (node.left != null) stack.push(node.left); //后压入左节点,先出栈 } return result; }
②后序遍历
public List<Integer> postorderTraversal(TreeNode root) { List<Integer> result = new ArrayList<>(); if(root == null) return result; Deque<TreeNode> stack=new ArrayDeque<>(); stack.push(root); while(!stack.isEmpty()){ TreeNode node=stack.pop(); result.add(node.val); //结点添加顺序为 根右左 if(node.left!=null) stack.push(node.left); if(node.right!=null) stack.push(node.right); } Collections.reverse(result); //反转为:左右根 return result; }
③中序遍历
中序遍历思路: 中序遍历迭代法思路不同于前序和后序.
①首先针对对当前节点,一直对其左子树迭代并将非空节点入栈
②节点指针迭代为空(到树底了)后不再入栈,然后取栈顶元素,存结果;
③将当前指针用出栈的节点的右子节点替代,然后回到第一步继续迭代,直到当前节点为空且栈为空.
public List<Integer> inorderTraversal(TreeNode root){ List<Integer> result = new ArrayList<>(); if(root==null) return result; Deque<TreeNode> stack = new ArrayDeque<>(); while (root!=null||!stack.isEmpty()){ while(root!=null){ stack.push(root); root=root.left; } TreeNode node=stack.pop(); result.add(node.val); root=node.right; } return result; }