0、前言:
线性表(一对一关系),每个元素之间只有一个直接前驱和一个直接后继。
树形结构(一对多关系),数据元素之间是层次关系,并且每一层的数据元素可能和下一层中多个元素相关,但只能和上一层中一个元素有关。(结点的孩子和双亲)
1、图(多对多关系)
图(Graph)是由顶点的有穷非空集合和顶点之间边的集合组成,通常表示为:G(V,E),其中,G表示一个图,V是图G中顶点的集合,E是图G中边的集合。在图中的数据元素,我们称之为顶点(Vertex),顶点集合有穷非空。在图中,任意两个顶点之间都可能有关系,顶点之间的逻辑关系用边来表示,边集可以是空的。
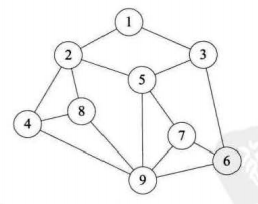
顶点:线性表中我们把数据元素叫元素,树中数据元素叫结点,在图中数据元素,我们则称之为顶点
边:线性表中,相邻的数据元素之间具有线性关系,树中,相邻两层的结点中具有层次关系,图中任意两个顶点之间都可能有关系,顶点之间的逻辑关系用边来表示
2、有向图和无向图
图按照边的有无方向分为无向图和有向图。无向图由顶点和边组成,有向图由顶点和弧构成。弧有弧尾和弧头之分,带箭头一端为弧头。

无向边:若顶点v1到v2之间的边没有方向,就是无向边,使用无序偶(,)(v1,v2)表示
有向边:若顶点v1到顶点v2的边有方向,则称这条边为有向边,又称为弧,使用有序偶<,><v1,v2>表示,其中v1为弧尾,v2为弧头,v1--->v2,有向边的两个顶点不能交换
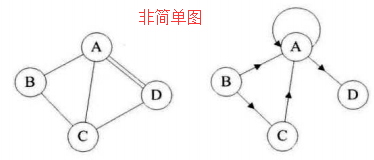
3、简单图
在图结构中,若不存在顶点到其自身的边,且同一条边不重复出现,则称图为简单图。
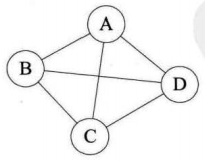
4、无向完全图和有向完全图
无向完全图:在无向图中,如果任意两个顶点之间都存在边,则称该图为无向完全图。有n个顶点的完全无向图有n(n-1)/2 条边
有向完全图:在有向图中,如果任意两个顶点之间都存在方向互为相反的两条弧,则称改图为有向完全图。含有n*(n-1)条边

5、稀疏图和稠密图
按照边或弧的多少来分稀疏图和稠密图。大于n*logn为稠密图,反之为稀疏图
6、网
有些图的边或弧具有与他相关的数字,这种与图的边或弧相关的数叫做权(Weight)。这些权可以表示从一个顶点到另一个顶点的距离或耗费。这种带权的图通常称为网(Network)

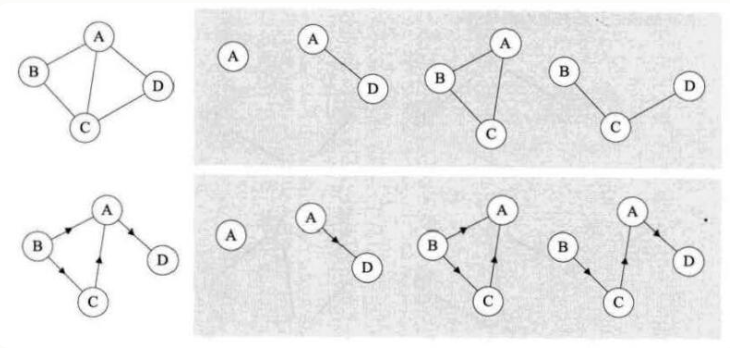
7、子图
假设有两个图G= (V,{E})和G'= (V',{E'}),如果V'是V的子集,且E'是E的子集,则称G'为G的子图。如下图带底纹的图均为左侧无向图与有向图的子图。