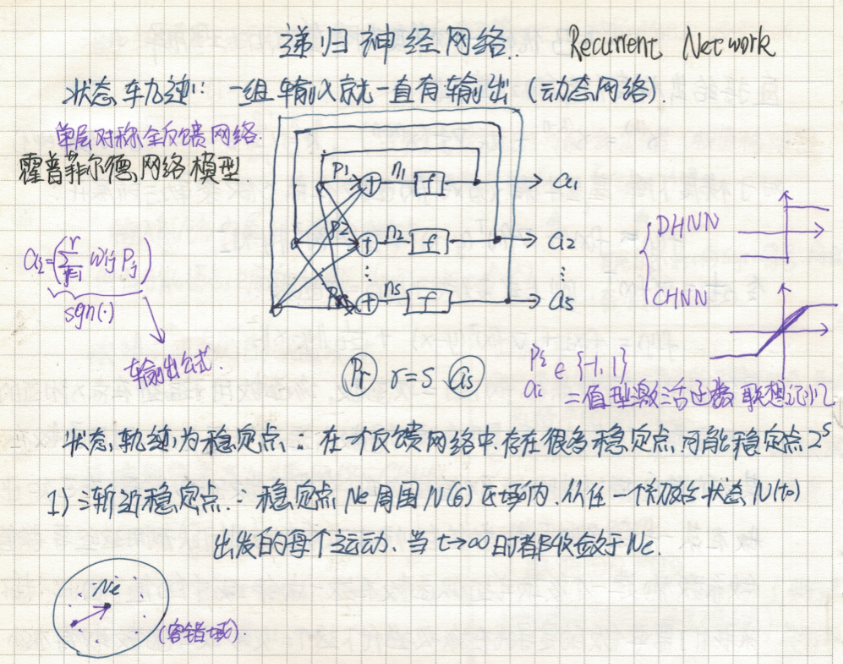


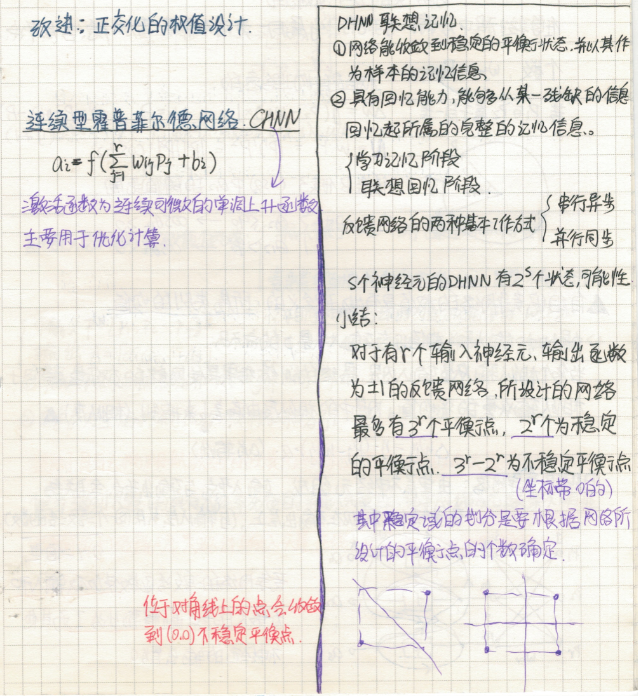
设计一个反馈网络存储下列目标平衡点:
T = [ 1 -1; -1 1 ];
并用6组任意随机初始列矢量,包括一组在目标平衡点连线的垂直平分线上的一点作为输入矢量对所设计的网络的平衡点进行测试,观察3次循环的每一次的输出结果。给出最后收敛到各自平衡点(或不稳定的平衡点)结果的次数。
采用正交化方法设计的霍普菲尔德网络结构,如下图:
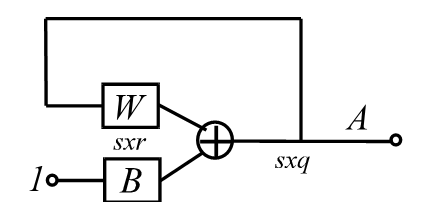
通过net=newhop(T);操作可得网络的权值和偏差为:
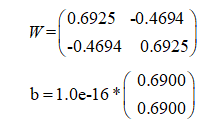
可见权值是对称的。
现在选取6组任意随机初始列矢量,并调整其中一组在目标平衡点连线的垂直平分线上,如下:
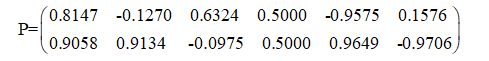
循环迭代60次效果如下图所示:
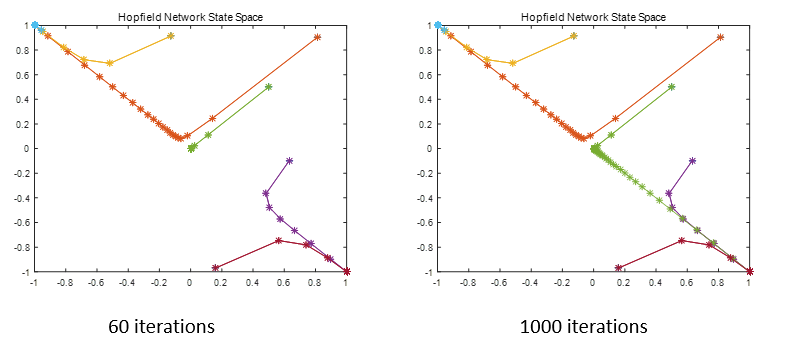
其中(0.5000,0.5000)点60次迭代收敛至不稳定平衡点(0,0),当迭代次数增大至1000时能改变这种情况。
最终收敛情况如下:


T=[1 -1;-1 1]; P=[ 0.8147 -0.1270 0.6324 0.5000 -0.9575 0.1576; 0.9058 0.9134 -0.0975 0.5000 0.9649 -0.9706]; net=newhop(T); W=net.lw{1,1} b=net.b{1} plot(T(1,:),T(2,:),'r*'); axis([-1 1 -1 1]) max_epoes =1000; [Y,Pf,Af] = sim(net,{6,max_epoes},[],P); plot(T(1,:),T(2,:),'*y'); hold on plot(P(1,:),P(2,:),'+'); hold on A=zeros(2,max_epoes+1); for i=1:6 for n=2:(max_epoes+1) A(1,n)=Y{n-1}(1,i); A(2,n)=Y{n-1}(2,i); hold on end A(1,1)=P(1,i); A(2,1)=P(2,i); title('Hopfield Network State Space') plot(A(1,:),A(2,:),'*-') end % for i=1:30 % A=sim(net,P); % P=A; % end % [a(1,i),aa(1,i)] % hold on % plot(aa(1,1),aa(2,1),'wx',aa(1,:),aa(2,:)) % Y_fanal=zeros(60,6); % for i=1:30 % [Y,Pf,Af] =net(6,[],P) % Y_fanal(i,:)=Y(1,:); % Y_fanal(i+1,:)=Y(2,:); % end % for i=1:6 % for j=1:2:30 % plot(Y_fanal(j,i),Y_fanal(j+1,i),'o-'); % hold on % end % end
