Farm Irrigation(HDU1198)(幷查集)

Submit Status

Description

Benny has a spacious farm land to irrigate. The farm land is a rectangle, and is divided into a lot of samll squares. Water pipes are placed in these squares. Different square has a different type of pipe. There are 11 types of pipes, which is marked from A to K, as Figure 1 shows.


Figure 1

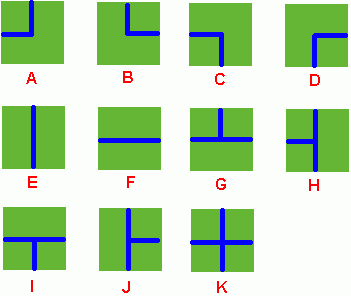
Benny has a map of his farm, which is an array of marks denoting the distribution of water pipes over the whole farm. For example, if he has a map

ADC
FJK
IHE

then the water pipes are distributed like


Figure 2

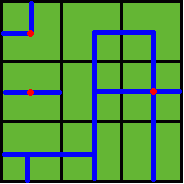
Several wellsprings are found in the center of some squares, so water can flow along the pipes from one square to another. If water flow crosses one square, the whole farm land in this square is irrigated and will have a good harvest in autumn.

Now Benny wants to know at least how many wellsprings should be found to have the whole farm land irrigated. Can you help him?

Note: In the above example, at least 3 wellsprings are needed, as those red points in Figure 2 show.

 

Input

There are several test cases! In each test case, the first line contains 2 integers M and N, then M lines follow. In each of these lines, there are N characters, in the range of 'A' to 'K', denoting the type of water pipe over the corresponding square. A negative M or N denotes the end of input, else you can assume 1 <= M, N <= 50.

 

Output

For each test case, output in one line the least number of wellsprings needed.

 

Sample Input

2 2
DK
HF

3 3
ADC
FJK
IHE

-1 -1

 

Sample Output

2
3

 

Hint

 

#include <iostream>
#include <algorithm>
using namespace std;
int a[500][500],p[500][500];
int n1,n2;
int map[11][4]={ 
    {1,0,0,1}, 
    {1,1,0,0}, 
    {0,0,1,1}, 
    {0,1,1,0}, 
    {1,0,1,0}, 
    {0,1,0,1}, 
    {1,1,0,1}, 
    {1,0,1,1}, 
    {0,1,1,1}, 
    {1,1,1,0}, 
    {1,1,1,1} 
};

int  p1(int q)
{if(p[q/n2][q%n2]==q)
return q;
else return p[q/n2][q%n2]=p1(p[q/n2][q%n2]);

}

void   v(int i,int j)
{
 
 
 

 if(map[a[i][j]][1]==1&&j<n2-1)
  if(map[a[i][j+1]][3]==1)
  {p[p1(p[i][j])/n2][p1(p[i][j])%n2]=p1(p[i][j+1]);
  v(i,j+1);}
  if(map[a[i][j]][2]==1&&i<n1-1)
   if(map[a[i+1][j]][0]==1)
   {p[p1(p[i][j])/n2][p1(p[i][j])%n2]=p1(p[i+1][j]);v(i+1,j);}
   
   return;}

void set()
{int i,j;
for(i=0;i<n1;i++)
for(j=0;j<n2;j++)
{p[i][j]=i*n2+j;}

}

void c()
{int y[2500];
int t=0,i,j;
for(i=0;i<n1;i++)
for(j=0;j<n2;j++)
{y[t]=p1(p[i][j]);t++;}
sort(y,y+n1*n2);
t=0;
for(i=1;i<n1*n2;i++)
if( y[i]!=y[i-1] )
t++;
printf( "%d ", (t+1) );

}

int main()
{
 int i,j;
 
 char l;
    while( scanf( "%d %d", &n1, &n2 ), n1>0&& n2> 0 )
  
 { 
  
  for(i=0;i<n1;i++)
   for(j=0;j<n2;j++)
   {    cin>>l;
   
   
   a[i][j]=int(l-'A');}
   set();
   
   for(i=0;i<n1;i++)
    for(j=0;j<n2;j++)
    {
     v(i,j);}
    c();
    
 }
 return 0; }