原创作品,转载请注明出处http://www.cnblogs.com/leo0000/p/5711576.html
自己写了有关了图的读入和无权最短路径和含有负边值的最短路径算法实现。
其中的迪杰斯特拉算法,求解无负边值的最短路径算法,没有写,因为还没有学习这个配对堆,当然不使用配对堆,使用优先队列也是可以的。
这个实现中涉及到了队列和散列表。有关优先队列或者说堆的一些操作可以看我的另一篇博客。
原图:
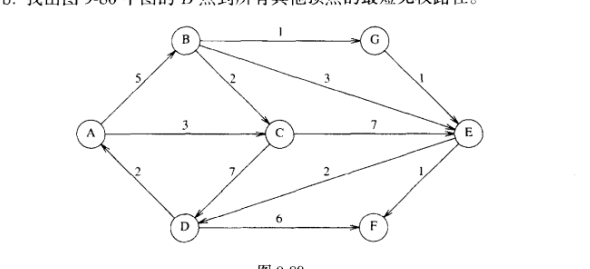
#include <stdio.h> #include <stdlib.h> #include <string.h> #include <math.h> typedef struct _queue { int cursor; int lastposition; int size; int *header; }queue; queue *queueinit(int size) { queue *ptQ = (queue *)malloc(sizeof(queue)); ptQ->cursor = 0; ptQ->lastposition = 0; ptQ->size = size; ptQ->header = (int *)malloc(sizeof(int)*size); return ptQ; } int Enqueue(int i,queue *ptQ) { if(ptQ->cursor-ptQ->lastposition == 1 || ptQ->lastposition - ptQ->cursor == ptQ->size -1) return -1; ptQ->header[ptQ->lastposition] = i; if(ptQ->lastposition == ptQ->size -1) ptQ->lastposition = 0; else ptQ->lastposition++; return i; } int Dequeue(queue *ptQ) { if(ptQ->cursor == ptQ->lastposition) return 0xffffffff; if(ptQ->cursor == ptQ->size -1) { ptQ->cursor = 0; return ptQ->header[ptQ->size-1]; } else { int tmp = ptQ->header[ptQ->cursor++]; return tmp; } } typedef enum _hashstat { empty = 0, occupied = 1, deleted = 2 }hashstat; #define namelen 100 typedef struct _hashentry { char name[namelen]; hashstat stat; }hashentry; typedef struct _hashtable { int tablesize; hashentry *table; }hashtable; int nextprime(int num) { int flags = 1; int i; do{ for(i = 2;i < sqrt((double)num);i++) if(num % i == 0) { num++; break; } if(i>=sqrt((double)num)) break; }while(flags); return num; } hashtable *hashinit(int tablesize) { if(tablesize < 10){ printf("tablesize is too small "); return 0; } tablesize = nextprime(tablesize); hashtable *tmp = (hashtable *)malloc(sizeof(hashtable)); tmp->tablesize = tablesize; tmp->table = (hashentry *)malloc(sizeof(hashentry)*tablesize); memset(tmp->table,0,sizeof(hashentry)*tablesize); return tmp; } int hash(char *key,int tablesize) { int tmp = 0; while(*key!= 0) tmp = (tmp<<5)+*key++; return tmp%tablesize; } int hashfind(char *key,hashtable *htable) { int position = 0; int collisionNum = 0; position = hash(key,htable->tablesize); while(htable->table[position].stat != empty && strcmp(key,htable->table[position].name) != 0) { position = position + 2*++collisionNum - 1; if(position >= htable->tablesize) position = position - htable->tablesize; } return position; } int hashinsert(char *key,hashtable *htable) { int position; position = hashfind(key,htable); if(htable->table[position].stat != occupied) { htable->table[position].stat = occupied; strcpy(htable->table[position].name,key); } return position; } void printhash(hashtable *htable) { for (int i = 0;i<htable->tablesize;i++) { if(htable->table[i].stat == occupied) printf("%s %d ",htable->table[i].name,i); } } typedef struct _node { int index; int distance; struct _node *next; }list,node; typedef struct _edge { char *s; char *d; int dist; }edge; typedef struct _tableentry { list *adjacentlist; int known; int p; int mindist; int degree; int hashval; }tableentry; typedef struct _graph { int nVertexNum; hashtable *htable; tableentry *AdjTable; }graph; void addadjacentvertex(tableentry *t,int i,int distance,graph *ptG) { node* tmp = 0; tmp = (node *)malloc(sizeof(node)); tmp->index = i; tmp->distance = distance; if(t->adjacentlist == 0) tmp->next = 0; else tmp->next = t->adjacentlist; t->adjacentlist = tmp; ptG->AdjTable[i].degree++; } void printpath(graph *ptG,int i) { if(ptG->AdjTable[i].p == 0){ printf("%s",ptG->htable->table[i].name); return; } printpath(ptG,ptG->AdjTable[i].p); printf("->%s",ptG->htable->table[i].name); } void printgraph(graph *ptG,int type)//type == 1 print adjacent list ;type == 2 print the minimum distance to the vertex that the distance is 0 { for(int i = 0;i<ptG->htable->tablesize;i++) if (ptG->htable->table[i].stat == occupied) { printf("%s : ",ptG->htable->table[i].name); if(type == 2) printf("mindist %d ",ptG->AdjTable[i].mindist); else if(type == 1){ node *cursor = ptG->AdjTable[i].adjacentlist; for(;cursor != 0; cursor = cursor->next){ if(type == 1) printf("%s ",ptG->htable->table[cursor->index].name); } printf(" "); } else if(type == 3) { printpath(ptG,i); printf(" "); } } } #define INFINITE 0xffffffff graph* initgraph2(edge e[],int edgeNum,int vertexNum) { graph *ptG = (graph *)malloc(sizeof(graph)); ptG->htable = hashinit(vertexNum); ptG->AdjTable = (tableentry *)malloc(sizeof(tableentry)*(ptG->htable->tablesize)); memset(ptG->AdjTable,0,sizeof(tableentry)*(ptG->htable->tablesize)); ptG->nVertexNum = vertexNum; int Shashposition; int Dhashposition; for(int i = 0;i<edgeNum;i++) { Shashposition = hashinsert(e[i].s,ptG->htable); ptG->AdjTable[Shashposition].hashval = Shashposition; ptG->AdjTable[Shashposition].mindist = INFINITE; Dhashposition = hashinsert(e[i].d,ptG->htable); ptG->AdjTable[Dhashposition].hashval = Dhashposition; ptG->AdjTable[Dhashposition].mindist = INFINITE; addadjacentvertex(&ptG->AdjTable[Shashposition],Dhashposition,e[i].dist,ptG); } //printhash(ptG->htable); printgraph(ptG,1); return ptG; } void unweightedpath(graph *ptG,char *key) { queue *ptQ = queueinit(ptG->nVertexNum); int i = hashfind(key,ptG->htable); if(ptG->AdjTable[i].hashval != i) return; Enqueue(i,ptQ); int position; node *cursor; int currdist = 0; ptG->AdjTable[i].mindist = 0; ptG->AdjTable[i].known = 1; while((position = Dequeue(ptQ)) != 0xffffffff) { cursor = ptG->AdjTable[position].adjacentlist; for(;cursor != 0;cursor=cursor->next) if(ptG->AdjTable[cursor->index].known == 0) { ptG->AdjTable[cursor->index].mindist = currdist + 1; ptG->AdjTable[cursor->index].known = 1; ptG->AdjTable[cursor->index].p = position; Enqueue(cursor->index,ptQ); } currdist++; } } void weightedpath(graph *ptG,char *key) { queue *ptQ = queueinit(ptG->nVertexNum); int i = hashfind(key,ptG->htable); if(ptG->AdjTable[i].hashval != i) return; Enqueue(i,ptQ); int position; node *cursor; int tmpdist = 0; ptG->AdjTable[i].mindist = 0; ptG->AdjTable[i].known = 1; while((position = Dequeue(ptQ)) != 0xffffffff) { cursor = ptG->AdjTable[position].adjacentlist; for(;cursor != 0;cursor=cursor->next) { tmpdist = ptG->AdjTable[position].mindist + cursor->distance; if(tmpdist < ptG->AdjTable[cursor->index].mindist || ptG->AdjTable[cursor->index].mindist == INFINITE) { ptG->AdjTable[cursor->index].mindist = tmpdist; ptG->AdjTable[cursor->index].known = 1; ptG->AdjTable[cursor->index].p = position; Enqueue(cursor->index,ptQ); } } } } int main() { graph *ptG; edge e[] ={ {"b","g",1}, {"a","b",5}, {"b","c",2}, {"b","e",3}, {"g","e",1}, {"a","c",3}, {"c","e",7}, {"d","a",2}, {"c","d",7}, {"e","d",2}, {"e","f",1}, {"d","f",6}, }; ptG = initgraph2(e,sizeof(e)/sizeof(edge),20); weightedpath(ptG,"a"); printgraph(ptG,3); //initgraph(); //topsort(); while(1); }