图论算法之查找强分支

原创作品，转载请注明出处http://www.cnblogs.com/leo0000/p/5713547.html 

之前已经写了有关图的最短路径算法，对比查找强分支的算法，个人觉得关键在于遍历时的顺序，是先序还是后序还是层序，中序没有使用到。

查找强分支的流程如下：

1.读入图，有两个读入算法，一个是原图，另一个是反向图

2.选取原图中的任意一个点开始后序遍历，如果图不是强连通的，那么需要多次后序遍历。后序遍历的操作是将该编号压入一个栈。即每棵树的根在栈顶。

3.选取上一步的栈顶元素中的标号，对反向图后序遍历，当然此时已经无所谓遍历次序，操作是将编号压入栈，当然其他数据结构也是可以的，返回上一层函数时如果有点还没有被遍历到，那么说明有多个强分支，向栈中压入一个0xffffffff，将各个强分支隔开，重复以上过程。

4.打印上一步中的栈。

有部分代码在上一篇博文中已给出，这边不再重复。

原图：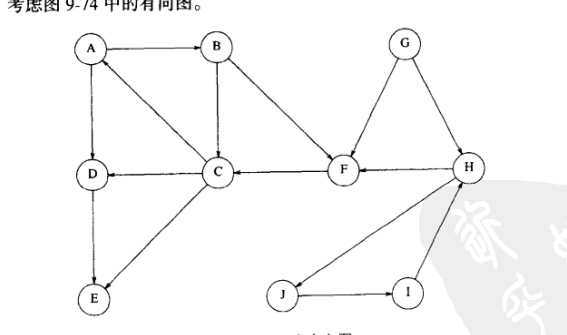

graph* initreversalgraph(edge e[],int edgeNum,int vertexNum)
{
    graph *ptGr = (graph *)malloc(sizeof(graph));
    ptGr->htable = hashinit(vertexNum*2);
    ptGr->AdjTable = (tableentry *)malloc(sizeof(tableentry)*(ptGr->htable->tablesize));
    memset(ptGr->AdjTable,0,sizeof(tableentry)*(ptGr->htable->tablesize));
    ptGr->nVertexNum = vertexNum;
    int Shashposition;
    int Dhashposition;

    for(int i = 0;i<edgeNum;i++)
    {
        Shashposition = hashinsert(e[i].d,ptGr->htable);
        ptGr->AdjTable[Shashposition].hashval = Shashposition;
        ptGr->AdjTable[Shashposition].mindist = INFINITE;
        Dhashposition = hashinsert(e[i].s,ptGr->htable);
        ptGr->AdjTable[Dhashposition].hashval = Dhashposition;
        ptGr->AdjTable[Dhashposition].mindist = INFINITE;
        addadjacentvertex(&ptGr->AdjTable[Shashposition],Dhashposition,e[i].dist,ptGr);
    }
    //printhash(ptG->htable);
    //printgraph(ptGr,1);
    return ptGr;
}

int count = 0;

void Num(graph *ptG,int i,int *pStack)
{
    node *cursor = ptG->AdjTable[i].adjacentlist;
    ptG->AdjTable[i].known = 1;
    for(;cursor != 0;cursor = cursor->next)
    {
        if(ptG->AdjTable[cursor->index].known == 0)
            Num(ptG,cursor->index,pStack);
    }
    pStack[++count] = i;
}

void printstack(int *Stack,hashtable *htable)
{
    for(int i = count;i>0;i--){
        if(Stack[i] == 0xffffffff)
            printf("
");
        else 
            printf("%s	",htable->table[Stack[i]].name);
    }
    printf("
");
}

void depthfirstgeneratetree(graph *ptG,int i,int *pStack)
{
    node *cursor = ptG->AdjTable[i].adjacentlist;
    ptG->AdjTable[i].known = 1; 
    for (;cursor != 0;cursor = cursor->next)
    {
        if (ptG->AdjTable[cursor->index].known == 0)
        {
            depthfirstgeneratetree(ptG,cursor->index,pStack);
        }
    }
    pStack[++count] = i;
}

void findstronglyconnected(graph *ptG,graph *ptGr)
{
    int Stack[20] = {0};
    int stringlyconnectedStack[20] = {0};
    int NumofsubStronglyConnectedGroup = 0;
    int i = -1;
    while(ptG->htable->table[++i].stat != occupied);
    Num(ptG,i,Stack);
    while(count < ptG->nVertexNum)
    {
        while(ptG->AdjTable[++i].known == 1);
        Num(ptG,i,Stack);
    } 
    //printstack(Stack);
    i = count;
    count = 0;
    depthfirstgeneratetree(ptGr,Stack[i],stringlyconnectedStack);
    NumofsubStronglyConnectedGroup++;
    while (count < ptGr->nVertexNum+NumofsubStronglyConnectedGroup)
    {
        stringlyconnectedStack[++count] = 0xffffffff;
        NumofsubStronglyConnectedGroup++;
        while(ptGr->AdjTable[Stack[--i]].known == 1);
        depthfirstgeneratetree(ptGr,Stack[i],stringlyconnectedStack);
    }
    printstack(stringlyconnectedStack,ptGr->htable);
}


int main()
{
    graph *ptG;
    graph *ptGr;
    /*edge e[] ={
        {"b","g",1},
        {"a","b",5},
        {"b","c",2},
        {"b","e",3},
        {"g","e",1},
        {"a","c",3},
        {"c","e",7},
        {"d","a",2},
        {"c","d",7},
        {"e","d",2},
        {"e","f",1},
        {"d","f",6},

    };
    edge e[] = 
    {
        {"b","g",1},
        {"a","b",1},
        {"b","c",1},
        {"b","e",1},
        {"g","e",1},
        {"a","c",1},
        {"c","e",1},
        {"d","a",1},
        {"c","d",1},
        {"e","d",1},
        {"e","f",1},
        {"d","f",1},
    };*/
    edge e[] = 
    {
        {"a","b",1},
        {"a","d",1},
        {"c","a",1},
        {"b","c",1},
        {"b","f",1},
        {"g","f",1},
        {"g","h",1},
        {"c","d",1},
        {"f","c",1},
        {"h","f",1},
        {"d","e",1},
        {"c","e",1},
        {"h","j",1},
        {"i","h",1},
        {"j","i",1},
    };
    ptG = initgraph2(e,sizeof(e)/sizeof(edge),10);
    ptGr = initreversalgraph(e,sizeof(e)/sizeof(edge),10);
    findstronglyconnected(ptG,ptGr);
    //weightedpath(ptG,"a");
    //printgraph(ptG,3);
    //initgraph();
    //topsort();
    while(1);
}