一、问题
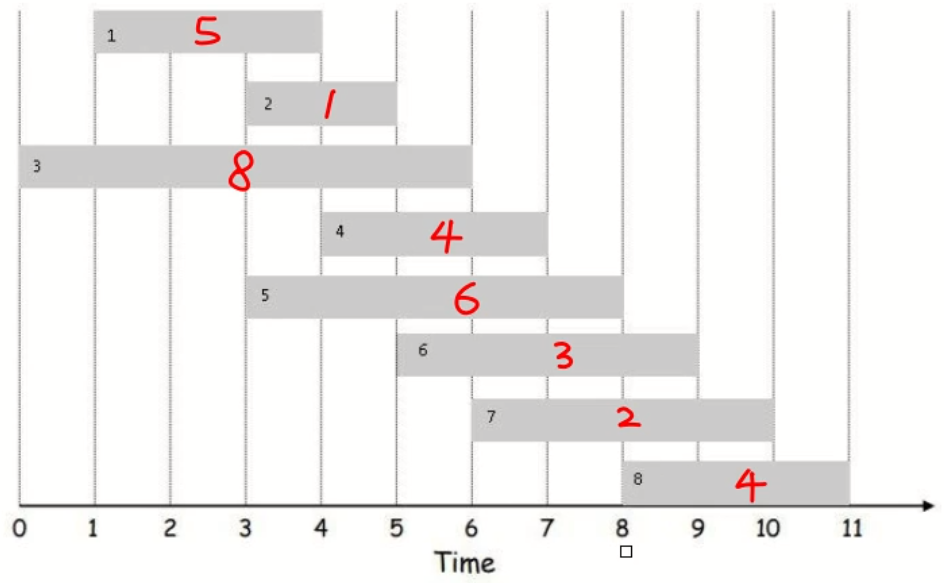
图中的8个灰色在柱状分别表示八份工作。所跨的宽度为做完该工作需要花费的时间。柱体中的红色手写数字为做完该份工作所能挣到的钱。
假设我们不能同时做有时间冲突的工作,问在0-11这个时间范围内,我们最多能挣多少钱?如何安排做哪些工作赚的钱最多。
二、分析问题
这是一个典型的可以使用动态规划(DP)来解决的问题。
1.找出递归规律
首先,我们假设我们一定要做第8份工作的时候,由于一定要做第8份工作,那么由于第6、7份工作与第8份工作有时间冲突,所以6、7不能做。
那么,我们在决定是否选择做第8份工作的时候,假设最大值为OPT(8)。
所以得到以下公式:

1)如果选择做第8份工作,则OPT(8) = val(8) + OPT(5) (因为一定要做8的话,前面最多能做到第5份工作)
2)如果不选择做第8份工作,则OPT(8) = OPT(7) (OPT(7)表示是否选择做7的最大收入)
3)我们在选与不选之间取他们的最大值,最终得到真正的OPT(8)
2.写出递归式

公式中的prev(i)就是一定要做第i份工作时,前面最近能做的某份工作的编号。例如prev(8) = 5。
prev是我们能够直接通过题目计算出来的:

有了prev表,我们的OPT就能够全部算出来了。
3.拆分计算过程
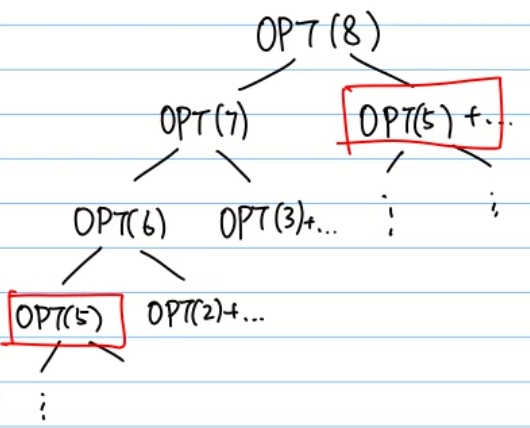
从图中可以看到,我们在求各个OPT的时候,左右分支上会出现Overlap Subproblem(重复子问题)。这个结构和斐波那契数列的递归求解是一样的。时间复杂度是O(2^n)。所以我们可以在计算过程中将这些子问题的结果记录下来(利用列表等)。
4.计算结果
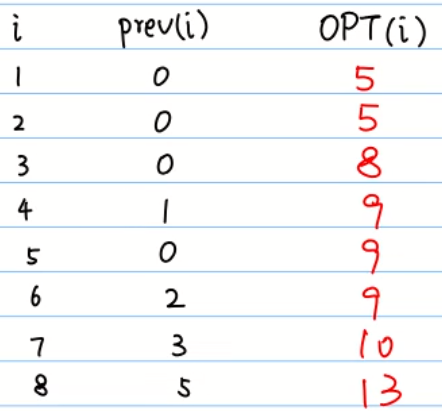
这样的话,我们求解OPT的时间复杂度就变成了O(n)。
我们计算的过程中,还可以将每一步的最优选择记录下来:

5.Python实现代码
import numpy as np def earnMore(data): data_len = len(data) # prev记录如果要做某个工作(index),前面最近的不冲突的工作的编号 prev_list = np.zeros(9, dtype=int) # 是否选择某份工作(index)时,能够达到的最大收益 opt_list = np.zeros(9, dtype=int) # 首先计算各个工作对应的prev,从8开始算 for i in range(len(data) - 1, 0, -1): start_time = data[i]['time'][0] for k in range(i - 1, 0, -1): end_time = data[k]['time'][1] if end_time <= start_time: prev_list[i] = k break # 从1开始计算OPT,记录到opt_list中 for i in range(1, len(data)): if i == 1: opt_list[i] = data[i]['val'] continue if prev_list[i] == 0: opt_list[i] = max(data[i]['val'], opt_list[i - 1]) else: opt_list[i] = max(data[i]['val'] + opt_list[prev_list[i]], opt_list[i - 1]) return opt_list if __name__ == '__main__': data = [ {}, {'val': 5, 'time': [1, 4]}, {'val': 1, 'time': [3, 5]}, {'val': 8, 'time': [0, 6]}, {'val': 4, 'time': [4, 7]}, {'val': 6, 'time': [3, 8]}, {'val': 3, 'time': [5, 9]}, {'val': 2, 'time': [6, 10]}, {'val': 4, 'time': [8, 11]} ] res = earnMore(data) print("规定时间内,所能达到的最大收入为",res[-1])
##