回溯算法类似于枚举过程,所不同的是,当发现现有的解已经不构成可行解时,回溯算法会退回到之前一个满足条件的节点(及时止损),继续尝试其他可能,从而大大减小了搜索空间。比如下面的四皇后问题。
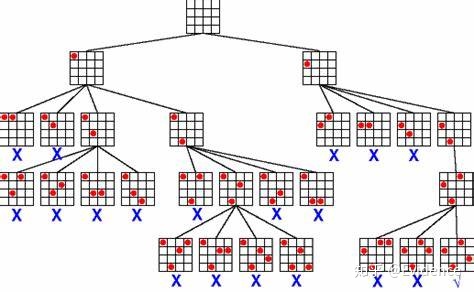
解题思路通常如下:
result = []
def backtrack(路径, 选择列表):
if 不可行解:
return
if 满足结束条件:
result.add(路径)
return
for 选择 in 选择列表:
做选择
backtrack(路径, 选择列表)
撤销选择
由于每次做选择的时候都要遍历当前条件下所有可能的选择,所以需要有一个撤销选择的操作。
太深的递归可能会造成栈溢出,而且也有效率问题,可以借助额外的栈实现非递归算法:
待补充...
全排列问题
求n个不重复数的所有全排列。
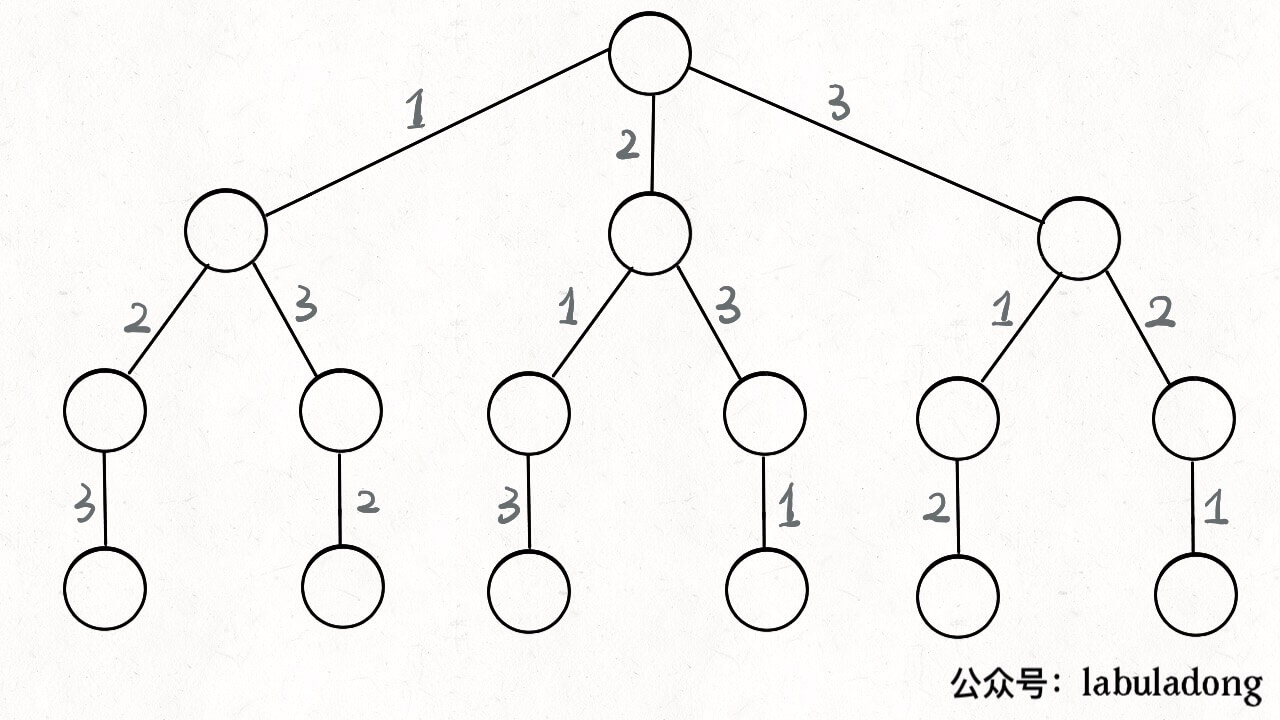
借助上文的模板,路径就是不同的排列,选择是路径外的数字,结束条件是路经长为n,因为候选解中已经确定为不相同的数字,所以不存在不可行解。
不推荐的例子:
result = []
n = 3
def backtrack(path: List[int], node: List[int]):
if len(path) == n:
result.append(path)
return
for x in node:
path_ = path.copy()
path_.append(x)
node_ = node.copy()
node_.remove(x)
backtrack(path_, node_)
backtrack([], list(range(n)))
print(result)
回溯算法的难点是如何设计路径和维护候选解集,设计的不好就容易造成实现起来复杂而且效率也不够高。比如以下给定没有重复数字的序列,返回所有可能的排列
输入: [1,2,3]
输出:
[
[1,2,3],
[1,3,2],
[2,1,3],
[2,3,1],
[3,1,2],
[3,2,1]
]
候选解并不一定要显示的给出,由于Python的可变对象的问题,通过当前的path推断可选的集合是更常用的选择。
class Solution:
def permute(self, nums: List[int]) -> List[List[int]]:
ans = list()
n = len(nums)
def backtrack(path):
if len(path) == n:
ans.append(path)
for x in nums:
if x not in path:
backtrack(path+[x])
backtrack([])
return ans
但如果是包含重复数字的排列,就不能简单的用重复数字找出候选集,此时就需要一个额外的visit列表记录该位置是否被访问过。
class Solution:
def permuteUnique(self, nums: List[int]) -> List[List[int]]:
nums.sort()
n = len(nums)
ans = list()
def backtrack(path: List[int], visit: List[bool]) -> None:
if len(path) == n:
ans.append(path)
else:
for i in range(n):
if (visit[i] == True or (i > 0 and nums[i] == nums[i-1] and visit[i-1] == False)):
pass
else:
visit[i] = True
backtrack(path+[nums[i]], visit)
visit[i] = False
backtrack([], [False]*n)
return ans