2019ICPC西安邀请赛 j And And And

题链接 https://nanti.jisuanke.com/t/39277

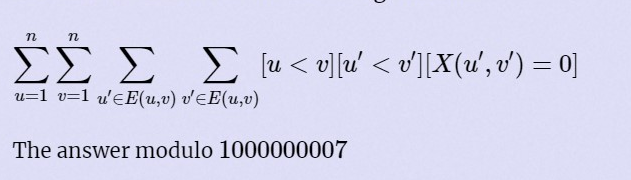
 好久不见我又回来了，这题要考虑他在问啥。这题要找子路径包含  异或和为0的路径   的路径的数量，而且有些许重复，枚举所有异或和为0 的路径，把他们的所有父路径列出来。

题解

如果x p在一条链子上，那就(siz[p])*( n - siz[x的儿子]),如果不在一条链子上，那就siz[x] * siz[p]; 值得注意的是，本题解选自https://blog.csdn.net/qq_42211531/article/details/96286606?utm_medium=distribute.pc_relevant_t0.none-task-blog-BlogCommendFromBaidu-1.nonecase&depth_1-utm_source=distribute.pc_relevant_t0.none-task-blog-BlogCommendFromBaidu-1.nonecase

看代码

#include<iostream>
#include<algorithm>
#include<vector>
#include<cstring>
#include<unordered_map>
using namespace std;
typedef long long ll;
const int maxn = 5e5 + 11;
const ll mod = 1000000007;

unordered_map<ll, ll>ins;
struct Node {
	int p;
	ll len;
	Node(int a, ll l) :p(a), len(l) {}
};

vector<Node>G[maxn];
void add(int x, int y,ll len) {
	G[x].push_back(Node(y, len));
}


ll chal[maxn];

ll siz[maxn];
int dfs(int x, int fa) {
	siz[x] = 1;
	for (int i = 0; i < G[x].size(); i++) {
		int p = G[x][i].p;
		ll len = G[x][i].len;
		if (p == fa) continue;
		chal[p] = chal[x] ^ len;
		dfs(p, x);
		siz[x] += siz[p];
	}
	return 0;
}
ll ans = 0;
int dfs1(int x, int fa) {
	ans = (ans + siz[x] * ins[chal[x]]) % mod;

	for (int i = 0; i < G[x].size(); i++) {
		int p = G[x][i].p;
		ll len = G[x][i].len;
		if (p == fa) continue;
		dfs1(p, x);
	}
	ins[chal[x]] += siz[x];
	return 0;
}
ll n;

int dfs2(int x, int fa) {
	ans = (ans + siz[x] * ins[chal[x]]) % mod;
	for (int i = 0; i < G[x].size(); i++) {
		int p = G[x][i].p;
		ll len = G[x][i].len;
		if (p == fa) continue;

		ins[chal[x]] += n - siz[p];

		dfs2(p, x);

		ins[chal[x]] -= n - siz[p];
	}
	return 0;
}
int main() {
	cin >> n;
	for (int i = 2; i <= n; i++) {
		int y;
		ll len;
		cin >> y >> len;
		add(i, y, len);
		add(y, i, len);
	}
	dfs(1, -1);
	ins.clear();
	dfs1(1, -1);
	ins.clear();
	dfs2(1, -1);
	printf("%lld
", ans);
	return 0;
}