文章目录
概述
基本推导和理论还是以看李航老师的《统计学习方法》为主。
各种算法的原理,推荐理解到可以手撕的程度。
以下为通过网络资源搜集整理的一些问题及答案,准备的有些仓促,没能记录所有资料的来源(侵删)
L1和L2的区别? 为什么L2能提升泛化能力(减少预测误差,防止过拟合?)
L2范数的规则项||W||2最小,可以使得W的每个元素都很小,都接近于0,但与L1范数不同,它不会让它等于0,而是接近于0,这里是有很大的区别的哦。而越小的参数说明模型越简单,越简单的模型则越不容易产生过拟合现象。为什么越小的参数说明模型越简单?我也不懂,我的理解是:限制了参数很小,实际上就限制了多项式某些分量的影响很小
L1会趋向于产生少量的特征,而其他的特征都是0,而L2会选择更多的特征,这些特征都会接近于0。Lasso在特征选择时候非常有用,而Ridge就只是一种规则化而已
L1正则化有哪些好处
• L1与L2的定义 https://getpocket.com/a/read/2314095436
• L1&L2的差别
• 使用场景
L1正则为什么可以把系数压缩成0,坐标下降法的具体实现细节
https://www.zhihu.com/question/37096933
https://www.jianshu.com/p/7b35bbb3478f
为什么要做数据归一化?
最优解的寻优过程明显会变得平缓,不拐弯,更容易正确的收敛到最优解
归一化方式
https://www.zhihu.com/question/20455227
交叉熵cross entropy损失函数?
假设两个概率分布p(x) 和q(x), H(p,q) 为cross entropy:
H(p,q)=−∑xp(x)logq(x)
0-1分类的交叉熵损失函数的形式
log loss是交叉熵的一个特例。 P(x)+q(x) =1

0-1分类为什么用交叉熵而不是平方损失?
负log似然
预测输出与 y 差得越多,L 的值越大,也就是说对当前模型的 “ 惩罚 ” 越大,而且是非线性增大,是一种类似指数增长的级别。这是由 log 函数本身的特性所决定的。这样的好处是模型会倾向于让预测输出更接近真实样本标签 y, 当误差越大,梯度就越大,参数w调整得越快,训练速度也就越快
在激活函数是sigmoid之类的函数的时候,用平方损失的话会导致误差比较小的时候梯度很小,这样就没法继续训练了,这时使用交叉熵损失就可以避免这种衰退。如果是线性输出或别的激活函数神经元的话完全可以用平方损失。
一般来讲,如果学习模型致力于解决的问题是回归问题的连续变量,那么使用平方损失函数较为合适;若是对于分类问题的离散Ont-Hot向量,那么交叉熵损失函数较为合适
https://blog.csdn.net/m_buddy/article/details/80224409
什么情况不用交叉熵?
回归问题
神经网络里面的损失函数有哪些
[TO-DO]
什么情况下一定会发生过拟合?
发生过拟合的主要原因可以有以下三点:
(1)数据有噪声
(2)训练数据不足,有限的训练数据 =>获取更多数据
(3)训练模型过度导致模型非常复杂 ,如因为特征过多等(一定)
解决过拟合的方法有哪些?
增加数据,减少模型复杂度->正则化
信息的定义
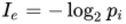
信息熵的定义
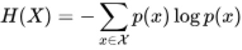
联合熵的定义
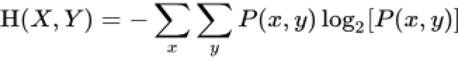
条件熵的定义
H(Y |X) = H(X,Y)−H(X) = -∑p(x)P(y|x)logp(y|x)
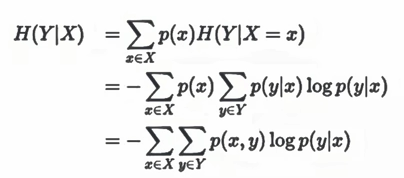
互信息(信息增益)的定义
I(X,Y) = H(X)+H(Y)−H(X,Y) = H(Y)−H(Y |X)