7-15 计算圆周率 (15分)

根据下面关系式，求圆周率的值，直到最后一项的值小于给定阈值。

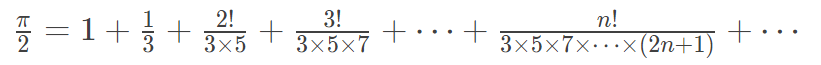
 有一个注意点是：该式的最后一项不要乘以2

自己写的C++代码

#include <iostream>
#include <iomanip>
using namespace std;

// 直接使用一个函数计算每一项的值，将每一项的值与阈值比较，如果小于阈值则跳出循环
double Factorial(int n) {
    if (n == 0) // 如果为0，直接返回1
        return 1;
    double numerator=1, denominator=1; // numerator为分子，denominator为分母
    for (int i = 1; i <= n; i++) { // 计算分子的值
        numerator *= i;
    }
    for (int j = 1; j <= 2*n+1; j += 2) { // 计算分母的值
        denominator *= j;
    }
    return numerator / denominator;
}

int main(void) {
    double precision, number=1, sum=0;
    int i = 0;
    cin >> precision;
    while (number > precision) {
        number = Factorial(i);
        sum += number;
        i++;
    };
    cout << setiosflags(ios::fixed) << setprecision(6) << 2 * sum;
    return 0;
}

网上写得不错的C代码

#include<stdio.h>
int main()
{
    int n = 0;
    double e, f;//e为输入的阈值，f为单独一项的值
    double fz = 1, fm = 1;//初始化分子，分母为1
    double sum = 0, pi;//sum为各项的和，pi为最终结果
    while (~scanf_s("%lf", &e))
    {
        for (f = 1; f >= e; n++)
        {
            if (n == 0)//第一项单独讨论
                fz = 1;
            else
                fz = fz * n;//后一项的分子等于前一项的分子乘上n
            fm = fm * (2 * n + 1);//后一项的分母等于前一项的分子乘上（2n+1）
            f = fz / fm;
            sum = sum + f;
        }
        pi = 2 * sum;
        printf("%.6f
", pi);
    }
    return 0;
}