定理
过$n$个有标志顶点的树的数目等于$n^{n-2}$。
此定理说明用$n-1$条边将$n$个已知的顶点连接起来的连通图的个数是$n^{n-1}$。也可以这样理解,将n个城市连接起来的树状网络有$n^{n-1}$种可能方案.所谓树状,指的是用$n-1$条边将$n$个城市连接起来,即无环。当然,建造一个树状网络一般是求其长度最短或造价最少等.Cayley定理只能说明可能方案的数目。
证明
Cayley定理的证明方法很多,下面采用最聪明也是最容易理解的一一对应法。不失一般性,假定已知的n个顶点标志为1,2,..n.
假设$T$是其中一棵树,树叶中有标号最小的,设为$a_1$,$a_1$的临界点为$b_1$,从图中消去$a_1$点和边$(a_1,b_1)$,$b_1$点便成为消去后余下的树$T_1$的顶点。在余下的树$T_1$中继续寻找标号最小的树叶,设为$a_2$,$a_2$的邻接点为$b_2$,从$T_1$中消去$a_2$及边$(a_2,b_2)$。如此步骤共执行n-2次,直到最后只剩下一条边为止.于是一棵树对应一序列
$$b_1,b_2,cdots ,b_{n-2}$$
$b_1,b_2,cdots ,b_{n-2}$是1到n的数,并且允许重复。
反过来从$b_1 b_2 cdots b_{n-2}$可以恢复树$T$本身,方法如下:
一个是顶点标号的有序序列
$$1,2, cdots ,n ag{1} $$
另一个是生成的序列
$$b_1,b_2,cdots ,b_{n-2} ag{2}$$
过程:在序列(1)中找出第一个不出现在序列(2)中的数,这个数显然便是$a_1$,同时形成的边$(a_1,b_1)$,并从(1)中消去$a_1$,从(2)中消去$b_1$,在余下的序列(1)、(2)中继续以上的步骤n-2次,直到序列(2)为空集为止。这时序列(1)剩下的两个数$a_k$,$b_k$,边$(a_k,b_k)$是树T的最后一条边。
以下图说明上述步骤:
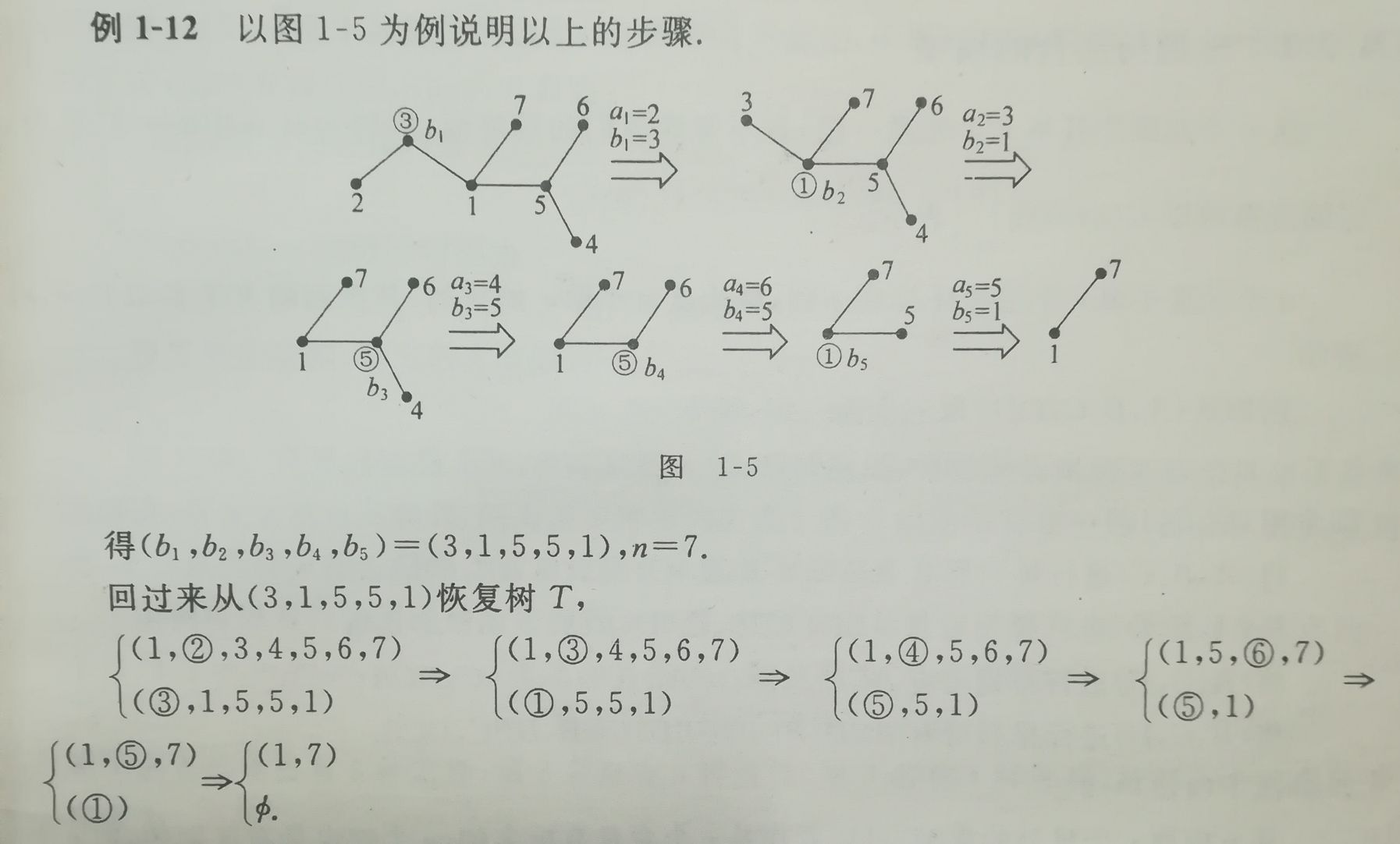
上面的过程说明过n个已知标号的顶点的树和序列$b_1b_2 cdots b_{n-2}$一一对应,根据乘法法则可得,过n个有标号(相当于互异)的顶点的树的数目,由于$1leq b_ileq n,i=1,2,cdots,n-2$,故为$n^{n-2}$个.
Cayley定理的证明过程实际上是提供了构造过n个有标号顶点的树的方法。
(参考书:组合数学 卢开澄、卢华明等编著)