杨表
在数学中,杨表(Young table)又称杨氏矩阵,最初用于对称群的表示理论。
杨图由有限个相邻的方格排列而成,其中,各横行的左边对齐,长度从上到下递增。分为英式画法和法式画法,这里只讨论标准杨表,
标准杨表:在杨图的n个方格中任意填入1到n中的相异正整数,各行和各列中的数字皆严格递增。
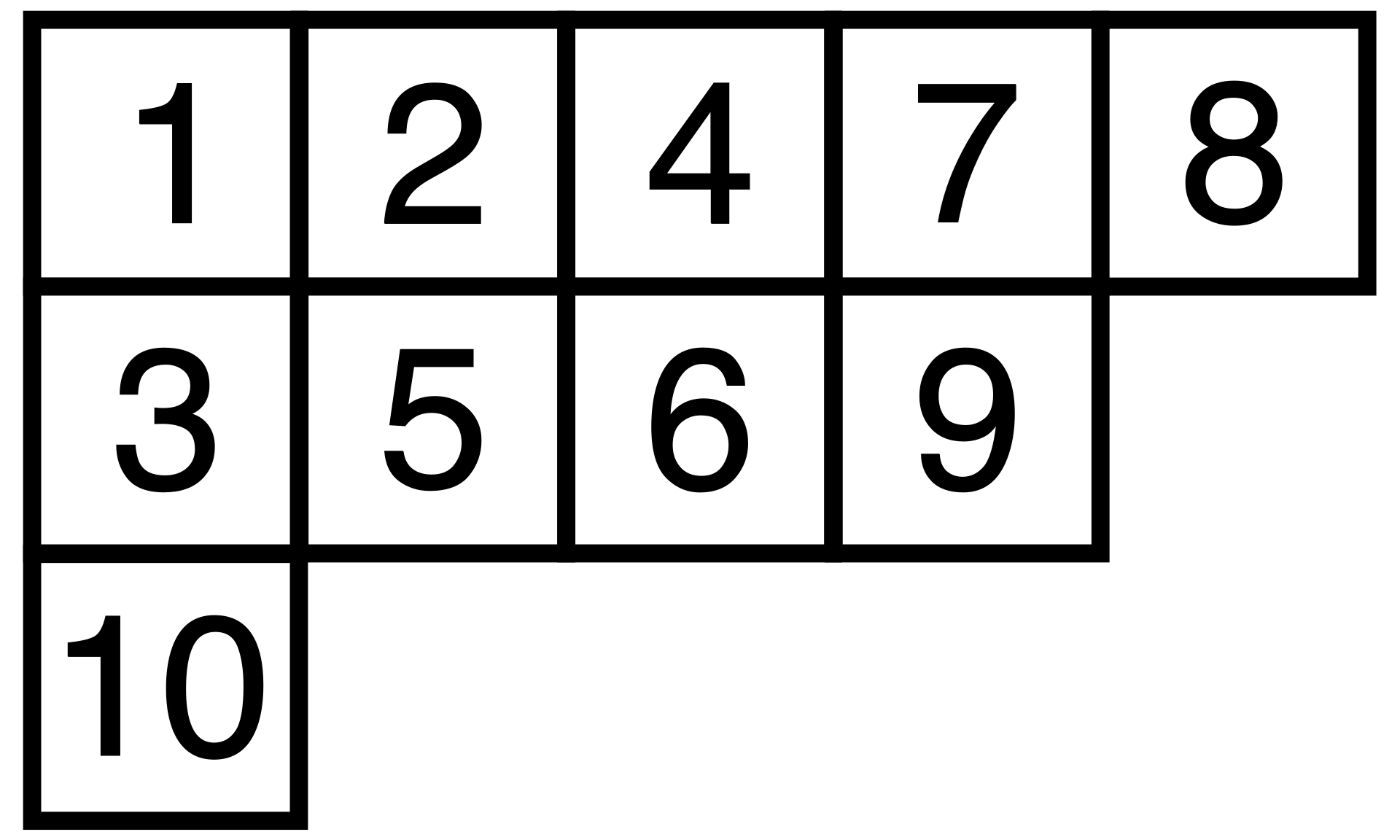
勾长、臂长、腿长
“臂长”是正右方的方格数,“腿长”是正下方的方格数,“勾长”是“臂长+腿长+1”
勾长公式
给定一个杨表πλ ,一共有n个方格。那么把1到n这n个数字填到这个杨表中,使得每行从左到右都是递增的,每列从下到上也是递增的(法式画法)。用 dimπλ 表示这样的方法个数。
勾长公式就是方法个数等于 n! 除以所有方格的勾长的乘积。
$$dimpi _lambda = frac{n!}{prod _{xin Y(lambda )}hook(x)}$$
例如,对于拆分10=5+4+1的杨表,
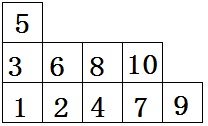
$$dimpi _lambda = frac{10!}{7cdot 5cdot 4cdot 3 cdot 1cdot 5cdot 3cdot 2cdot 1 cdot 1 = 288 }$$
n个方格的标准杨表个数
1,1,2,4,10,26,76,232,764,2620,9496,...(OEIS中的数列A000085)
递推形式为:$f(n) = f(n-1) + (n-1)*f(n-2), f(0)=1, f(1)=1$
例如,n=3 时
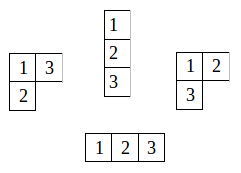
例子
问题:1-16十六个数字分别填入十六格方框内,要求从左至右的数字是从小到大排列,从上至下的数字也是从小到大排列,问:有多少种排列方式。
分析:
这实际上一个杨氏矩阵问题。
直接使用勾子公式,
按照4*4矩阵的形状,反对角线上的格子的钩子长度是一样的,

所以最终答案是:
$16!/(7*6^2*5^3*4^4*3^3*2^2*1)=24024$
参考链接:
1. https://zh.wikipedia.org/wiki/%E6%9D%A8%E6%B0%8F%E7%9F%A9%E9%98%B5