一、什么是并查集?
并查集是一种用来管理元素分类的情况的数据结构,并查集可以高效的进行如下操作:
查询元素a和b是否属于同一组
合并元素a和元素b所在的组
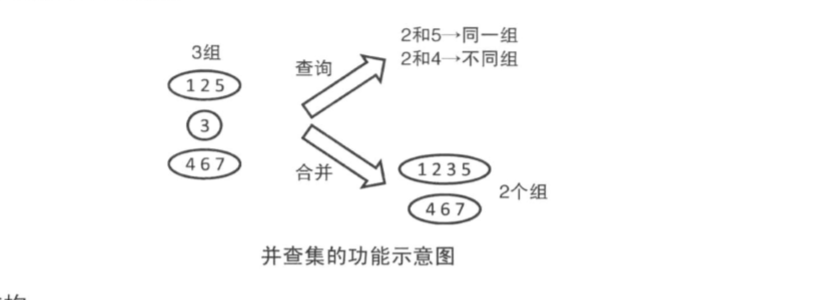
但不方便进行分割操作
二、并查集的结构
并查集也是使用树形结构实现的,不过,不是二叉树
每个元素对应一个节点,每个组对应一棵树。在并查集中哪个节点是哪个节点的父亲以及树的形状等信息无需多加关注,整体形成一颗树形结构才是重要的。
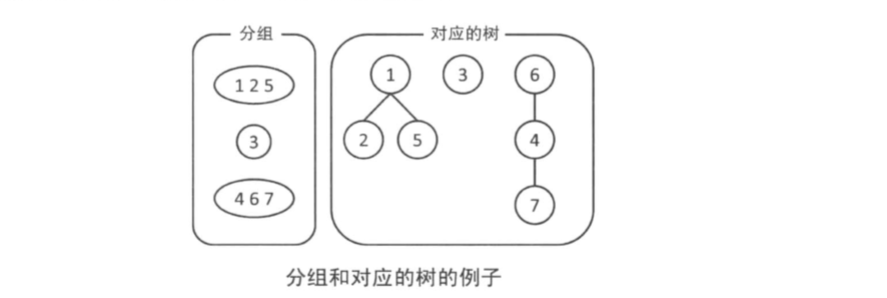
(1)初始化
我们准备n个节点来表示n个元素,最开始没有边(为了判断根节点,每个节点添加一条指向相同节点的边)

(2)查询
为了查询两个节点是否属于同一组,我们只需判断两者的根节点是否相同。
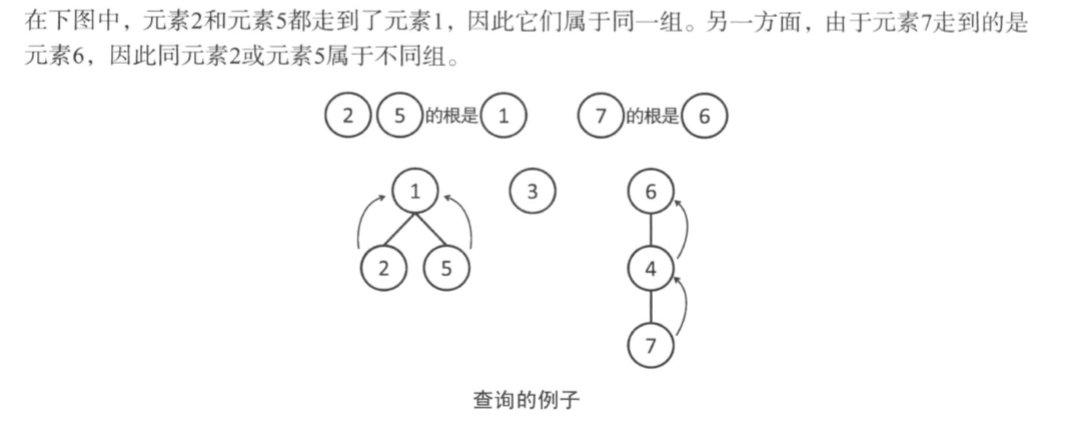
(3)合并
从一个组的根向另一个组的根连边,这样两棵树就变成了一棵树,也就把两个组合成了一个组了。
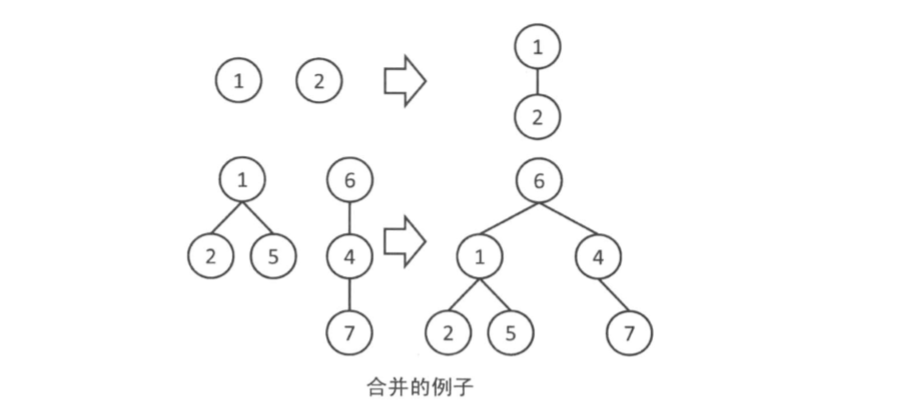
三、并查集实现中的注意点
在树形结构里,一旦退化成链式结构,那么复杂度就会变得很高。因此有必要想办法避免退化的发生。
(1)对于每棵树记录这棵树的高度(rank)
合并时如果两棵树的rank不同,那么从rank小的向rank大的连边。
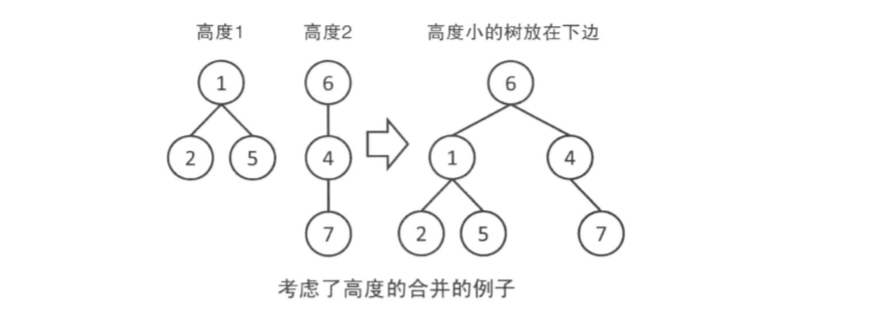
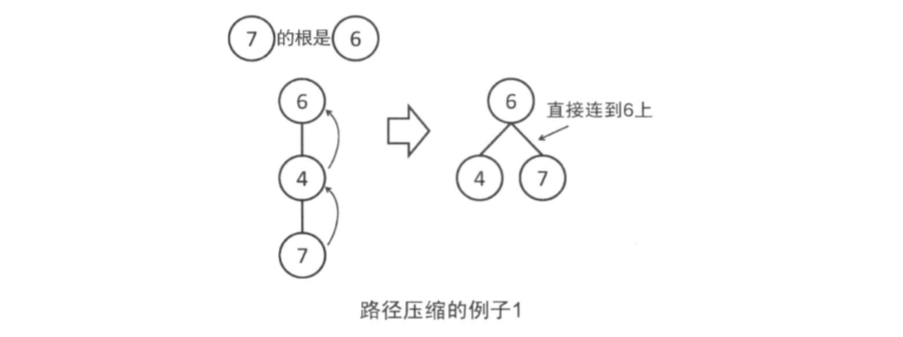
(2)此外,也可以通过路径压缩
对于每个节点,一旦向上走到了一次根节点,就把这个点到父亲的边改为直接指向根。
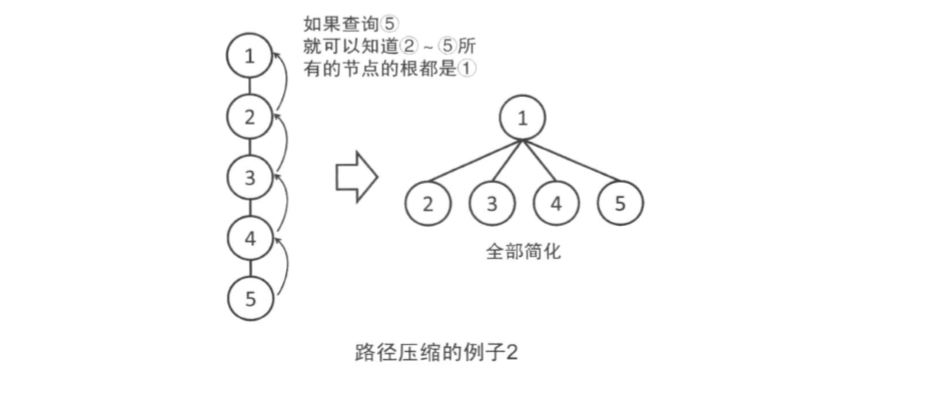
在此之上,不仅仅是所查询的节点,在查询过程中向上经过的的所有节点,如果不是直接连到根上,都改为直接连到根上。
这样再次查询这些节点时,就可以很快知道根时谁了。
在使用这种方法时,为了简单起见,即使树的高度发生了变化,我们也不修改rank的值,即方法一与方法二使用其中一个就可以了
方法二简化的效率高,而且便于编写,推荐使用方法二。
四、并查集的复杂度(平均复杂度)
加入这两个优化后的并查集效率非常高。对n个元素的并查集进行一次操作的额复杂度是O(α(n)),α(n)是阿克曼(Ackermann)函数的反函数。这比O(log(n))还要快。
五、并查集的代码实现
我们用编号代表每个元素,数组par表示父节点的编号,fa[x] = x是,说明x是所在树的根节点。
1 const int maxn = 100000 + 10; 2 int fa[maxn]; //fa父节点 3 4 //初始化n个节点 5 void init(int n) 6 { 7 for (int i = 0; i <= n; i++) 8 fa[i] = i; 9 } 10 11 //查询树的根 12 int find(int x) 13 { 14 if (x != fa[x]) 15 return fa[x] = find(fa[x]); 16 return fa[x]; 17 } 18 19 //合并x和y所属的集合 20 void unite(int x, int y) 21 { 22 int rx = find(x); 23 int ry = find(y); 24 if (rx == ry) return; 25 26 fa[rx] = ry; 27 } 28 29 //判断x和y是否属于同一集合 30 bool same(int x, int y) 31 { 32 return find(x) == find(y); 33 }