poj_1330Nearest Common Ancestors

Nearest Common Ancestors

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 14185		Accepted: 7571

Description

A rooted tree is a well-known data structure in computer science and engineering. An example is shown below: 

 
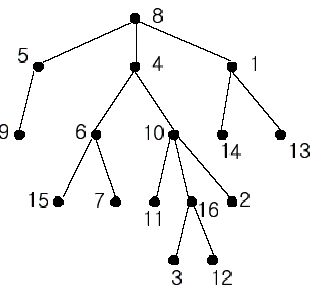
In the figure, each node is labeled with an integer from {1, 2,...,16}. Node 8 is the root of the tree. Node x is an ancestor of node y if node x is in the path between the root and node y. For example, node 4 is an ancestor of node 16. Node 10 is also an ancestor of node 16. As a matter of fact, nodes 8, 4, 10, and 16 are the ancestors of node 16. Remember that a node is an ancestor of itself. Nodes 8, 4, 6, and 7 are the ancestors of node 7. A node x is called a common ancestor of two different nodes y and z if node x is an ancestor of node y and an ancestor of node z. Thus, nodes 8 and 4 are the common ancestors of nodes 16 and 7. A node x is called the nearest common ancestor of nodes y and z if x is a common ancestor of y and z and nearest to y and z among their common ancestors. Hence, the nearest common ancestor of nodes 16 and 7 is node 4. Node 4 is nearer to nodes 16 and 7 than node 8 is. 

For other examples, the nearest common ancestor of nodes 2 and 3 is node 10, the nearest common ancestor of nodes 6 and 13 is node 8, and the nearest common ancestor of nodes 4 and 12 is node 4. In the last example, if y is an ancestor of z, then the nearest common ancestor of y and z is y. 

Write a program that finds the nearest common ancestor of two distinct nodes in a tree. 

Input

The input consists of T test cases. The number of test cases (T) is given in the first line of the input file. Each test case starts with a line containing an integer N , the number of nodes in a tree, 2<=N<=10,000. The nodes are labeled with integers 1, 2,..., N. Each of the next N -1 lines contains a pair of integers that represent an edge --the first integer is the parent node of the second integer. Note that a tree with N nodes has exactly N - 1 edges. The last line of each test case contains two distinct integers whose nearest common ancestor is to be computed.

Output

Print exactly one line for each test case. The line should contain the integer that is the nearest common ancestor.

Sample Input

2
16
1 14
8 5
10 16
5 9
4 6
8 4
4 10
1 13
6 15
10 11
6 7
10 2
16 3
8 1
16 12
16 7
5
2 3
3 4
3 1
1 5
3 5

Sample Output

4
3

测试模版，仅仅一次查询，本没必要用LCA解决的

#include <iostream>
#include <vector>
#include <cstdio>
#include <cstring>
using namespace std;
#pragma warning(disable : 4996)

const int MAX = 10005;
int father[MAX];//表示x的父节点
int ranks[MAX];//表示x的秩
int indegree[MAX];//保存每个节点的入度
bool visited[MAX];//标记访问
vector<int> tree[MAX], Ques[MAX];
int ancestor[MAX];

void init(int n)
{
	for(int i = 1; i <= n; i++)
	{

		ranks[i] = 1;
		father[i] = i;
		indegree[i] = 0;
		visited[i] = false;
		ancestor[i] = 0;
		tree[i].clear();
		Ques[i].clear();
	}

}

int find(int x)
{
	if(x != father[x])
	{
		father[x] = find(father[x]);
	}
	return father[x];
}//查找函数，并压缩路径

int Union(int x, int y)
{
	x = find(x);
	y = find(y);
	if(x == y)
	{
		return 0;
	}
	//相等的话,x向y合并
	else if(ranks[x] <= ranks[y])
	{
		father[x] = y;
		ranks[y] += ranks[x];
	}
	else
	{
		father[y] = x;
		ranks[x] += ranks[y];
	}
	return 1;

}//合并函数，如果属于同一分支则返回0，成功合并返回1

void LCA(int u)
{
	int size;
	ancestor[u] = u;
	size = tree[u].size();
	for(int i = 0; i < size; i++)
	{
		LCA(tree[u][i]);
		Union(u, tree[u][i]);
		ancestor[find(u)] = u;
	}
	visited[u] = true;
	size = Ques[u].size();
	for(int i = 0; i < size; i++)
	{
		//如果已经访问了问题节点,就可以返回结果了.
		if(visited[Ques[u][i]])
		{
			printf("%d\n", ancestor[find(Ques[u][i])]);
			return;
		}
	}
}

int main()
{
	freopen("in.txt", "r", stdin);
	int cnt, n, x, y;
	scanf("%d", &cnt);
	while(cnt--)
	{
		scanf("%d", &n);
		init(n);
		for(int i = 1; i < n; i++)
		{
			scanf("%d %d", &x, &y);
			tree[x].push_back(y);
			indegree[y]++;
		}
		//这里可以输入多组询问
		scanf("%d %d", &x, &y);
		//相当于询问两次
		Ques[x].push_back(y);
		Ques[y].push_back(x);
		for(int i = 1; i <= n; i++)
		{
			//寻找根节点
			if(indegree[i] == 0)
			{
				LCA(i);
				break;
			}
		}
	}
	return 0;
}