题目大意 (Description)
给定一棵树,求合法的集合 ({ A,B,C }) 的个数。一个集合是合法的当且仅当不存在任意一条路径同时覆盖 (A,B,C) 三个点。
题解 (Solution)
如果直接按题目大意做很难处理其约束条件,不妨反面思考。问题转化为:求树上有多少组({ A,B,C})三个节点可以被同一条路径覆盖。
考虑固定其中一个点,那么它同以它某个子节点 (v) 为根的子树内的某个点(以下称为第(1)类点),和除以 (v) 为根的子树外的某个点(以下称为第(2)类点)构成一条路径。枚举这个点,同时记录一个 (sz_i) 数组表示以它为根的子树大小。那么对于树上的某个节点 (u) ,第一类点有 (sz_v) 个,第二类点有 (n-sz_v-1) 个,由乘法原理,节点 (u) 对答案的贡献即为 $ sumlimits_{v in son_u} sz_v (n-sz_v-1)$ 。
但是照着上面的式子直接上是会 (WA) 的,原因如下图(纯手绘,图丑勿喷):
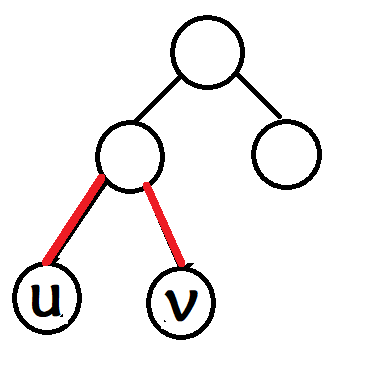
可以看出,(u) 节点到 (v) 节点的路径在枚举他们的 (LCA) 的时候被重复计算了,所以为了防止被重复计算,在我们枚举一个点 (u) 时,同时维护一个 nowsum ,初始化为 nowsum=n,每次计算完以 (u) 的子节点 (v) 为根的子树后减去 (sz_v) ,最终答案即为 ({n choose 3} - sumlimits_{u=1}^{n}sumlimits_{v in son_u} sz_v ( nowsum - sz_v - 1)),参考代码如下。
非 (std) 的代码(仅供参考)
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll N=1e5+50;
ll n,sz[N],head[N],cnt,sum,ans;
inline ll read()
{
ll sum=0,f=1;
char ch=0;
while(!isdigit(ch))
{
if(ch=='-') f=-1;
ch=getchar();
}
while(isdigit(ch))
{
sum=sum*10+(ch^48);
ch=getchar();
}
return sum*f;
}
inline void write(ll x)
{
if(x<0)
{
x=-x;
putchar('-');
}
if(x>9) write(x/10);
putchar(x%10+'0');
}
struct edge
{
int to,nxt;
}e[N<<1];
inline void add(int u,int v)
{
e[++cnt].to=v;
e[cnt].nxt=head[u];
head[u]=cnt;
}
void dfs(int u,int fa)
{
sz[u]=1;
int nowsum=n;
for(int i=head[u];i;i=e[i].nxt)
{
int v=e[i].to;
if(v==fa) continue;
dfs(v,u);
sum+=sz[v]*(nowsum-sz[v]-1);//乘法原理统计答案
nowsum-=sz[v];
sz[u]+=sz[v];//同时更新sz[u]
}
}
int main(void)
{
n=read();
for(int i=1;i<n;i++)
{
int u=read(),v=read();
add(u,v),add(v,u);
}
dfs(1,-1);
ans=n*(n-1)*(n-2)/6;//即C(n,3),注意不能预处理阶乘,因为题目没有取模
write(ans-sum);
putchar('
');
return 0;
}