切糕(cut)
【问题描述】
小R意外获得了一块切糕,他准备把切糕分给n个小伙伴。切糕的形状是一个底边长为a,高为b的等腰三角形。小R打算横着或竖着切n-1刀把切糕切成面积相等的n块分给小伙伴,请你告诉他要在哪些地方切。
【输入格式】
输入文件cut.in
输入包含四个整数n,a,b,c,表示要切成n块,切糕的三个顶点分别位于(0,0),(a,0),(a/2,b),若c=0,表示要横着切;若c=1,表示要竖着切。
【输出格式】
输出文件cut.out
输出共n-1行,每行一个实数,从小到大输出各切割处的位置,若c=0,每输出一个整数a,表示在直线y=a处切一刀;若c=1,每输出一个整数a,表示在直线x=a处切一刀。当你的输出与标准输出的绝对误差不超过时,判为正确。
【样例输入1】
3 5 2 0
【样例输出1】
0.3670068381
0.8452994616
【样例输入2】
2 5 3 1
【样例输出2】
2.5
【数据范围】
对于全部数据,2<=n<=1000,1<=a,b<=10^5;
对于50%的数据,c=0;
对于另外50%的数据,c=1。
暴力解方程
我们先分析横着的,设三角形AEF底为a,高为h,面积为S
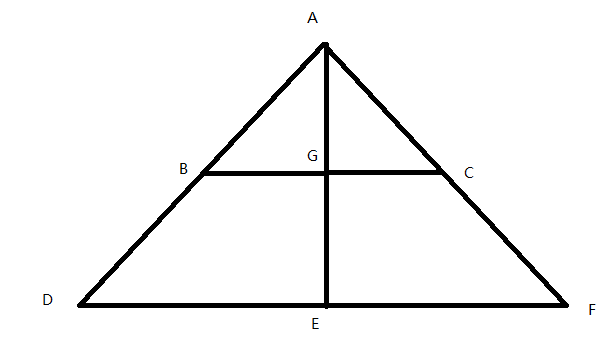
AG,AE为三角形ABC,ADF的高,BC是我们要砍的第i刀
我们设AG=x ∵△ABC∽△ADE ∴AG^2/AE^2=S△ABC/S△ADF
(x^2)/(h^2)=((1-i/n)*S)/S
答案为GE=AE-AG=h-x
然后来分析竖着的
AG,DE为三角形ABC,BDE的高,DE是我们要砍的第i刀
(1)i<=n/2
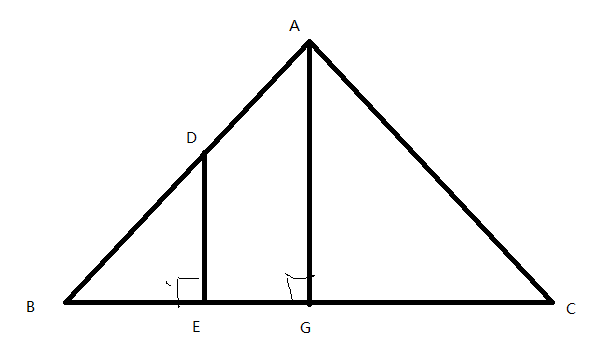
设BE=x ∵△BDE∽△BAG ∴BE^2/BG^2=S△BDE/S△BAG
(x^2)/((a/2)^2)=((i/n)*S)/(S/2)
x^2=(i/n)*2*(a/2)^2
x=(a/2)*sqrt((i/n)*2)
答案为BE=x
(2)i>n/2
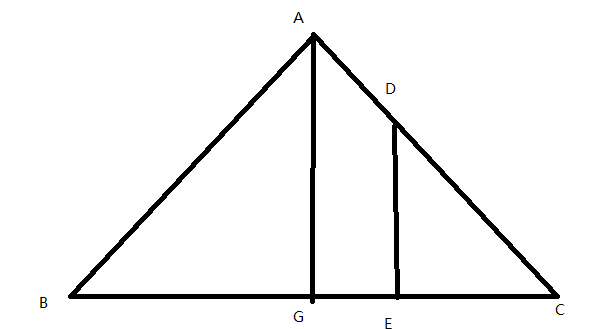
设CE=x ∵△CDE∽△CAG ∴CE^2/CG^2=S△CDE/S△CAG
(x^2)/((a/2)^2)=((1-i/n)*S)/(S/2)
x^2=(1-i/n)*2*(a/2)^2
x=(a/2)*sqrt((1-i/n)*2)
答案为BE=BC-CE=a-x
时间复杂度O(n)

#include<iostream> #include<cstdio> #include<cmath> using namespace std; double a,h;int n,c; int main() { //freopen("cut.in","r",stdin); //freopen("cut.out","w",stdout); cin>>n>>a>>h>>c; for(int i=1;i<n;i++) { if(!c)printf("%.10lf ",h-h*sqrt(1-(double)i/n)); else { if(i<=n/2)printf("%.10lf ",(a/2.0)*sqrt((double)i*2/n)); else printf("%.10lf ",a-(a/2.0)*sqrt((1-(double)i/n)*2)); } } return 0; }
采购(buy)
【问题描述】
小R有一个爱好,他经常去杂货市场上采购一些奇奇怪怪的物品。今天小R来到市场,发现有n个摊位,每个摊位出售不同的货物,第i个摊位出售的货物价格为ai。这些摊位的老板很奇怪,他们不喜欢你购买其他摊位的物品,如果你购买了k件其他摊位的物品,你在购买第i个摊位出售的物品时需要额外支付k*bi的钱,为了防止你买完一个摊位的物品后再去买另一家的物品,他们商量好要求你同时结账,现在小R有m元钱,他想知道自己最多能买多少种不同的物品。每个摊位只卖一种物品。
【输入格式】
输入文件buy.in
第一行两个正整数n和m,表示摊位数和小R的钱数。
接下来n行,每行两个非负整数ai,bi,意义同问题描述。
【输出格式】
输出文件buy.out
输出一个非负整数,表示答案。
【样例输入】
3 7
1 3
2 1
3 0
【样例输出】
2
【数据范围】
对于20%的数据,n<=20;
对于40%的数据,n<=1000;
对于另外10%的数据,bi=0;
对于另外20%的数据,所有bi均相等;
对于100%的数据,n,ai,bi<=100,000,m<=10^9。
二分答案k,当k已知时,每个摊位出售的物品价格是可以算出来的,c[i]=a[i]+b[i]*(k-1)(不算自己摊位买的商品)
我们把c数组按从小到大的顺序排序,买最前面的k样商品,看看总价钱有没有超过m,有就减小k,没有就增加k
本题会爆int,记得开long long
时间复杂度O(nlog(n)^2)

#include<iostream> #include<cstdio> #include<algorithm> using namespace std; long long c[100001];int a[100001],b[100001]; int n;long long m; bool cmp(int a,int b){return a<b;} bool check(int k) { long long mm=m; for(int i=1;i<=n;i++)c[i]=((long long)a[i]+(long long)b[i]*(k-1)); sort(c+1,c+n+1); for(int i=1;i<=k;i++){mm-=c[i];if(mm<0)return false;} return true; } int main() { //freopen("buy.in","r",stdin); //freopen("buy.out","w",stdout); cin>>n>>m; for(int i=1;i<=n;i++) { scanf("%d%d",&a[i],&b[i]); } int l=1,r=n+1; while(l<r) { int mid=(l+r)/2; if(check(mid))l=mid+1; else r=mid; } printf("%d",l-1); return 0; }
能量(power)
【问题描述】
小R在某次杂货采购中买到了n个XOR能量石,每个能量石有一个能量系数ai和共鸣系数bi,其中能量系数决定了能量石的好坏。小R想知道这些能量石的品质,但能量系数无法简单观测得到,只有通过能量共鸣仪促使能量石之间发生共鸣,才有办法获知能量系数。能量共鸣仪每次可以使一个区间内的所有能量石发生共鸣,并且获知这些能量石能量系数的异或和,但需要消耗等同于区间内所有能量石共鸣系数异或和的能量。小R已经测量出了各个能量石的共鸣系数,现在他想知道至少需要多少能量才能确定所有能量石的能量系数。
【输入格式】
输入文件power.in
第一行一个正整数n,表示能量石的个数。
第二行n个整数bi,表示各个能量石的共鸣系数。
【输出格式】
输出文件power.out
输出一个整数,表示最小的能量花费。
【样例输入】
2
1 3
【样例输出】
3
【数据范围】
对于20%的数据,n<=10;
对于50%的数据,n<=100;
对于70%的数据,n<=1,000;
对于100%的数据,n<=10,000,0<=bi<2^31。
下面的^表示异或
先介绍几个异或的性质
a^b=b^a
a^b=c => c^b=a
a^b^c=a^(b^c)
如果我们知道了每个石头能量系数的前缀异或和(aa[]),那么我们就可以算出每个石头的能量系数 a[i]=aa[i]^aa[i-1]
然后,我们如果知道了aa[x-1],那么我们可以通过获取[x,y]的异或和来得到aa[y] (x<y) aa[x-1]^[x,y]=aa[y] (前缀异或和的定义)
同理,我们如果知道了aa[y],那么我们可以通过获取[x,y]的异或和来得到aa[x-1] (x<y) aa[y]^[x,y]=aa[x-1]
题目要 求和的最小值,我们想到了什么,对,最小生成树
我们可以进行以下连边:开一个0号节点(aa[0]=0(前0个数的前缀异或和为0)),从x-1向y连一条b[x]^……^b[y]的无向边(知道aa[x-1]后,就能推出aa[y])
为了方便处理,我们预处理出每个石头的共鸣系数的前缀异或和(bb[])
这样,我们使得这棵树连通,就能求出aa数组
因为边数过多(n*(n-1)条),所以我们不能用Kruskal求最小生成树,只能使用Prim,且Prim不能使用堆优化,一是更新答案时也要O(n),二是会爆空间
时间复杂度O(n^2),由于附中机子跑得快,所以还是能过

#include<iostream> #include<cstdio> #include<cstring> using namespace std; int b[10001],bb[10001],n,d[10001];long long ans=0; bool used[10001]; int main() { // freopen("power.in","r",stdin); // freopen("power.out","w",stdout); scanf("%d",&n); for(int i=1;i<=n;i++) { scanf("%d",&b[i]);bb[i]=b[i]^bb[i-1]; } memset(d,127,sizeof(d));d[0]=0; for(int i=0;i<=n;i++) { int v=-1; for(int j=0;j<=n;j++)if(!used[j]&&(v==-1||d[j]<d[v]))v=j; ans+=d[v];used[v]=1; for(int j=0;j<=n;j++)d[j]=min(d[j],bb[j]^bb[v]); } cout<<ans; return 0; }
