三元环

对无向图的三元环计数。

先对所有无向边定向，从度数小的点连向度数大的点，度数相同时，从编号小的点连向编号大的点。枚举每一个点 (x)，将其连出的点 (y) 都打上 (x) 的标记，再枚举点 (y) 连出的点 (z)，若点 (z) 有 (x) 的标记，则 ((x,y,z)) 为一个三元环。

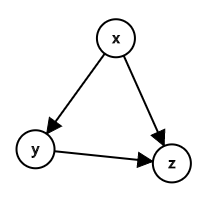
这样每个三元环只会在 (x) 处统计一次。

for(int i=1;i<=m;++i)
{
    int x=ed[i].x,y=ed[i].y;
    if(deg[x]>deg[y]||(deg[x]==deg[y]&&x>y)) swap(x,y);
    add(x,y);
}
for(int x=1;x<=n;++x)
{
    for(int i=head[x];i;i=e[i].nxt) vis[e[i].to]=x;
    for(int i=head[x];i;i=e[i].nxt)
        for(int j=head[e[i].to];j;j=e[j].nxt)
            if(vis[e[j].to]==x)
                ans++;
}

定向后的图是不存在环的，因为如果存在环，则环上的每个点度数都相同，且编号都相同，这样的情况是不存在的。

枚举的过程中，(x longrightarrow y) 这条边对复杂度的贡献为 (y) 的出边个数 (out_y)，得总贡献为 (sumlimits_{i=1}^m out_{y_i})。

当 (deg_y leqslant sqrt m) 时，得 (out_y) 是 (O(sqrt m)) 的。

当 (deg_y > sqrt m) 时，因为度数和是 (O(m)) 的，度数大于 (deg_y) 的点的个数是 (O(sqrt m)) 的，得 (out_y) 是 (O(sqrt m)) 的。

所以复杂度为 (O(m sqrt m))。