Codeforces Round #647 (Div. 1) - Thanks, Algo Muse!
A
权值从小到大填,确定一个点的权值后,更新其相邻点的 (operatorname{mex})。
B
先将 (k_i) 从大到小排序,将 (p_{k_i}) 分到当前和较小的集合中,相等时分到第一个集合中,这样做就能只让出现次数为奇数的 (k_i) 产生贡献,因此差值最小。记录模意义下的差值来判定相等,用两个不同模数来防止误判。
C
枚举最终答案 (k),把给定的线看作点,将两端珍珠权值在模 (2^k) 意义下相等的线之间连边,若存在欧拉回路,则该答案合法,方案即为欧拉回路。
D
发现该树的形态为若干条链在根节点处相接。设点 (i) 到根节点的距离为 (d_i),其为链上第 (j) 远的点,得其贡献为 ((k-j-(j-1))d_i)。考虑 (k-j-(j-1)) 的正负,当其 (geqslant 0),即 (j leqslant frac{k+1}{2}) 时,一定是先选距离远的,当其 (<0),即 (j > frac{k+1}{2}) 时,一定是先选距离近的。那么在每条链上选出贡献前 (k) 大的的点,排序后取前 (k) 大的和即为答案。
E
当以点 (x) 的 (dfs) 树上只有返祖边时,点 (x) 是有趣的。因为条件为 (20\%) 的点,所以只要随机撒点 (100) 次,每次 (O(n+m)) 判断当前点是否有趣,即可判定是否有解,每次错误的概率为 (frac{4}{5})。
找到一个有趣的点后,在其为根的 (dfs) 树上,对于除了根节点的一个点 (x),有两条性质:
(x) 的子树内必须恰好有一条返祖边经过 (x),否则 (x) 不是有趣的点。
满足上一条的情况下,(x) 为有趣的当且仅当 (x) 的子树内的返祖边指向的点为有趣的。
第一条性质不难证明,考虑证明第二条:
充分性:(x) 能通过树边到达其子树内的所有点,通过仅有的返祖边到 (y),因为 (y) 是有趣的,所以 (x) 能到达其子树外的所有点。
必要性:当 (x) 为有趣的时,考虑以 (x) 为根的 (dfs) 树,在原树中 (x) 子树外的部分,(y) 是有趣的,因为当前的 (dfs) 树和这部分只有返祖边,所以 (y) 对于原树中 (x) 子树内的部分也是有趣的。
可以树上差分处理每个点被返祖边覆盖的情况,同时记录每个点子树内返祖边指向深度最浅的点,即可推出其他的有趣的点。
F
每个 (W_i) 会控制一个以该位置为最小值的极大区间,每次操作会交换该位置两侧的区间。因此考虑对 (W_i) 建笛卡尔树,(P_i) 挂在叶子节点上。
当 (P = [3, 4, 6, 2, 1, 5],W = [5, 2, 3, 1, 4]) 时,对应的笛卡尔树为:
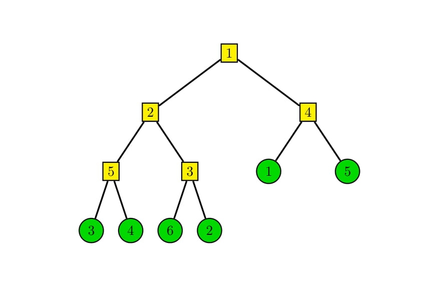
发现操作就转化为了交换笛卡尔树上的左右儿子,设 (val_x) 为 (x) 左子树对于右子树的逆序对个数,考虑是否交换左右儿子,得 (x) 的最小贡献为:
在每个节点上用权值线段树维护子树内的 (P_i) 即可,因为数据随机,所以期望树高为 (O(log n)),每次修改就暴力跳父亲,复杂度为 (O(n log^2 n))。