目录
一、特征的定义
二、Harris角点检测原理
1.灰度变化描述
2.E(u,v)E(u,v)简化
3.如何度量角点响应
三、实现Harris角点检测
OpenCV可以检测图像的主要特征,然后提取这些特征、使其成为图像描述符,这类似于人的眼睛和大脑。这些图像特征可作为图像搜索的数据库。此外,人们可以利用这些关键点将图像拼接起来,组成一个更大的图像,比如将许多图像放在一块,然后形成一个360度全景图像,这里我使用python+OpenCV来检测图像角点特征
一 特征定义
什么是特征?粗略的讲,特征就是有意义的图像区域,该区域具有独特特征和易于识别性。因此角点及高密度区域都是很好的特征,而大量重复的模式或低密度区域(例如图像中的蓝色天空)则不是很好的特征。边缘可以将图像分为两个区域,因此也可以看做好的特征。大多数特征检测算法都会涉及图像的角点的识别,由于某些算法在识别和提取某类型特征的时候有较好的效果,所以知道输入图像是什么很重要,这样做有利于选择最合适的OpenCV工具包。
二 Harris角点检测原理
什么是角点?
角点是一类具有特定特征的点,角点也是处在一个无论框框往哪边移动 框框内像素值都会变化很大的情况而定下来的点
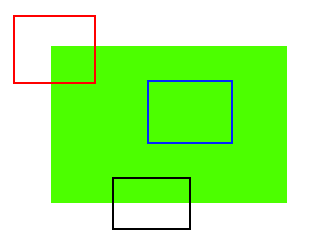
如上图有三个颜色的框框,如果我们对蓝色框框进行移动,无论是水平还是垂直的方向移动都不会对框框内像素造成很大的变化,这种是内部区域
如果我们对黑色的框框进行移动,那么水平方向上移动像素值是不会有什么太大的变化的,如果是垂直方向上移动那么就会变化很大,这种一般称为边缘区域
最后的重点,我们对红色的框框进行移动,无论是往哪个方向进行偏移都会对框框内的像素值造成很大的变动,那么红色框框框住的区域的边角点,我们就称为角点
Harris角点检测的基本思想:算法基本思想是使用一个固定窗口在图像上进行任意方向上的滑动,比较滑动前与滑动后两种情况,窗口中的像素灰度变化程度,如果存在任意方向上的滑动,都有着较大灰度变化,那么我们可以认为该窗口中存在角点。
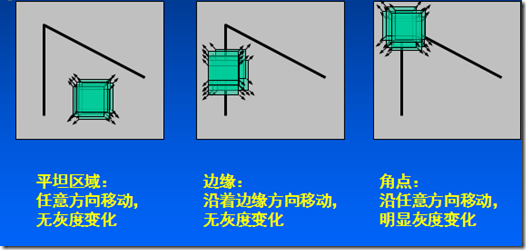
1、灰度变化描述
当窗口发生[u,v][u,v]移动时,那么滑动前与滑动后对应的窗口中的像素点灰度变化描述如下:

其中:[u,v][u,v]是窗口WW的偏移量;(x,y)(x,y)是窗口WW所对应的像素坐标位置,窗口有多大,就有多少个位置;I(x,y)I(x,y)是像素坐标位置(x,y)(x,y)的图像灰度值;I(x+u,y+v)I(x+u,y+v)是像素坐标位置(x+u,y+v)(x+u,y+v)的图像灰度值;w(x,y)w(x,y)是窗口函数,最简单情形就是窗口WW内的所有像素所对应的ww权重系数均为1.但有时候,我们会将w(x,y)w(x,y)函数设置为以窗口WW中心为原点的二元正太分布。如果窗口WW中心点是角点时,移动前与移动后,该点在灰度变化贡献最大;而离窗口WW中心(角点)较远的点,这些点的灰度变化几近平缓,这些点的权重系数,可以设定小值,以示该点对灰度变化贡献较小,那么我们自然使用二元高斯函数来表示窗口函数;
2、E(u,v)E(u,v)化简
首先需要了解泰勒公式,任何一个函数表达式,均可有泰勒公式进行展开,以逼近原函数,我们可以对下面函数进行一阶展开

所以E(u,v)E(u,v)表达式可以更新为:


3、如何度量角点响应
通常用下面表达式进行度量,对每一个窗口计算得到一个分数R,根据R的大小来判定窗口内是否存在harris特征角。分数R根据下面公式计算得到:
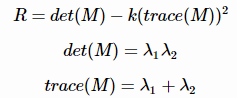
这里λ1,λ2λ1,λ2是矩阵M的2个特征值,kk是一个指定值,这是一个经验参数,需要实验确定它的合适大小,通常它的值在0.04和0.06之间,它的存在只是调节函数的形状而已。
R取决于M的特征值,对于角点|R||R|很大,平坦的区域|R||R|很小,边缘的R为负值;

如何通过矩阵判断角点的? 其实上面,已经推导出E(u,v)E(u,v)的表达式,看看这个表达式其中矩阵M是实对称矩阵,那么E表达式其实就是二次型,uu,vv代表窗口滑动方向以及滑动量,EE代表灰度变化,通过矩阵M进行特征值求解,而特征值所对应的特征向量即为灰度变化方向。如果两个特征值较大,则表示有两个方向灰度变化较快。所以可以直接通过求解MM的特征值进行角点判断.
三 实现Harris角点检测
Harris角点检测可以分为5个步骤:
1、计算图像I(x,y)I(x,y)在xx和yy两个方向的梯度IxIx,IyIy;
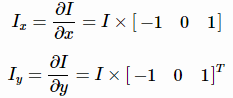
2、计算图像两个方向梯度的乘积;

3、使用高斯函数对I2xIx2、I2yIy2、IxIyIxIy进行高斯加权(取σ=2,ksize=3),计算中心点为(x,y)(x,y)的窗口WW对应的矩阵MM;

4、计算每个像素点(x,y)处的(x,y)处的Harris响应值RR;
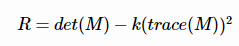
5、过滤大于某一阈值tt的RR值;

代码实现
# -*- coding: utf-8 -*-
from pylab import *
from PIL import Image
from PCV.localdescriptors import harris
"""
Example of detecting Harris corner points (Figure 2-1 in the book).
"""
# 读入图像
im = array(Image.open(r'C:UsersLEPycharmProjectsuntitledlight_1.jpg').convert('L'))
# 检测harris角点
harrisim = harris.compute_harris_response(im)
# Harris响应函数
harrisim1 = 255 - harrisim
figure()
gray()
#画出Harris响应图
subplot(141)
imshow(harrisim1)
print harrisim1.shape
axis('off')
axis('equal')
threshold = [0.01, 0.05, 0.1]
for i, thres in enumerate(threshold):
filtered_coords = harris.get_harris_points(harrisim, 6, thres)
subplot(1, 4, i+2)
imshow(im)
print im.shape
plot([p[1] for p in filtered_coords], [p[0] for p in filtered_coords], '*')
axis('off')
show()
第一组:纹理平坦
正面图

运行结果

正面远图

运行结果:

旋转图

运行结果:

有光线图

运行结果:

侧面图

运行结果:

结论:在纹理平坦的图片中,近远图对比角点数基本一样,旋转图与原图的区别不大,侧面的检测角点数大于正面 ,光亮很强时检测不到角点,墙面的棱角也会被检测到。
第二组:边缘多图
正面图

运行结果

远景图

运行结果

侧面图

运行结果

亮光线图

运行结果:

旋转图

运行结果

结论:与正面图相比,侧面图角点少一点,远景图和旋转图差别不大,亮光线图角点会多一点点
第三组:角点丰富图
正面图

运行结果

旋转图

运行结果:

近景图

运行结果

亮光线图

运行结果:

远景图

运行结果:

结论:与正面图相比,近景图和旋转图没有太大差别,远景图角点较多,亮光线图角点较少。
小结:
①观察得到:我将这三组实验阈值分别设为0.01,0.05,0.1,由实验结果可看出,每一组的实验都随着阈值的增加,检测到的角点逐渐减少。
②遇到的问题:刚开始读几张超高清图片时出现RuntimeWarning: invalid value encountered in dividereturn Wdet / Wtr这样的报错 ,一直不知道什么原因浪费了很多时间,后来百度得知图片转换为矩阵时发生溢出,改小图片像素得以解决。还有图片路径的问题,一定不要直接粘贴复制,需要手动敲写,不然也会报错。
分析:
k为阈值
假设已经得到了矩阵M的特征值λ1≥λ2≥0λ1≥λ2≥0,令λ2=αλ1λ2=αλ1,0≤α≤10≤α≤1。由特征值与矩阵M的直迹和行列式的关系可得:
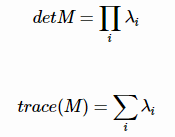
从而可以得到角点的响应:

假设R≥0,则有:
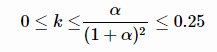
对于较小的α值:
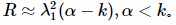
由此,可以得出结论,增大k的值,降低角点检测的灵敏度,减少被检测角点的数量;减少k值,增加角点检测的灵敏度,增加被检测角点的数量。
四、总结:
1.计算简单:Harris 算子中只用到灰度的一阶差分以及滤波,操作简单。
2.提取的点特征均匀而且合理:Harris 算子对图像中的每个点都计算其兴趣值,然后在邻域中选择最优点。在纹理信息丰富的区域,Harris 算子可以提取出大量有用的特征点,而在纹理信息少的区域,提取的特征点则较少。
3.稳定:Harris算子的计算公式中只涉及到一阶导数,因此对图像旋转、灰度变化不太敏感,是比较稳定的一种点特征提取算子。
