手算平方根的「正确」方法,是什么方法?如果你认为是牛顿迭代法的话,你可以亲自试一下,看看效果如何:
(原帖 kz3007407872, 鉴于百度贴吧的帖子是公开的,我就不打码了)
其实牛顿迭代法非常好,在电脑上快得飞起。但是手算就不行了。
那么「正确」的方法是什么呢?是这个:
(原帖同上)
说得神神叨叨的,还能开无限小数,到底是什么方法?帖子里没说。
不过,幸运的是,我有一天翻 Wiki 的时候,碰巧翻到了这个方法。本文将详细介绍这个方法。
(2) 的算术平方根是多少?是 (sqrt{2}). 不是 (1.41), 也不是 (1.414213). 所以,本文讨论的计算,是以(十进制小数)近似值为主的。准确地说,是不足近似值。
近似值,无论是精确到小数点后 1 位还是 1000 位,都是近似值。所以,计算近似值,先得确定精度(即:你算到哪一 位 / 数量级 就满意了)。
先讨论对一位数开平方,精确到小数点后 1 位的情况(以计算 (sqrt{2}) 为例)。
这一上来就有一个问题:大家都知道 (sqrt{2}) 精确到一位小数是 (1.4), 但为是么是 (1.4), 不是 (1.3) 或 (1.5)?
显然,(1.5^2 > 2), 不是我们要的不足近似值。而 ( 1.3^2 < 1.4^2 < 2 ) 所以在不过剩的情况下,最接近的(在给定精度范围内的)数是 (1.4).
既然是这样的话,我们就可以把这个过程「概括」成这样一个问题的求解:
求最大的一位数 (x), 使得不等式 ( overline{1.x}^2 leqslant 2 ) 成立。
求出 (x=4) 后,如果要继续提高精度,那么再求解这个问题:
求最大的一位数 (y), 使得不等式 ( overline{1.4y}^2 leqslant 2 ) 成立。
(精度还可以继续提高)
……
这其实就是大家计算平方根最常用的方法,即「试乘」。但是计算 ( overline{1.x} ) 的平方,是多位数乘多位数,不好算。而且随着精度增加,越来越难算((overline{1.414213x}^2) 什么的,想想就要爆炸)。既然硬算不好算,那么就需要技巧。什么技巧呢?我们可以把式子变形一下,来降低运算的规模:
( (1+frac{x}{10})^2 leqslant 2 ) (1)
把完全平方展开,得:
( 1+frac{2x}{10}+frac{x^2}{100} leqslant 2 )
( Leftrightarrow frac{2x}{10}+frac{x^2}{100} leqslant 1 )
( Leftrightarrow 20x+x^2 leqslant 100 )
( Leftrightarrow x(20+x) leqslant 100 )
( Leftrightarrow xcdot overline{2x} leqslant 100 ) (2)
这样,运算规模就从多位数乘多位数降低到了一位数乘多位数,立马好算了许多。
继续提高精度,求百分位上的数字 (y):
( (1+frac{x}{10}+frac{y}{100})^2 leqslant 2 )
( Leftrightarrow {left [(1+frac{x}{10})+frac{y}{100} ight ]}^2 leqslant 2 )
( Leftrightarrow (1+frac{x}{10})^2+2(1+frac{x}{10})frac{y}{100}+frac{y^2}{10000} leqslant 2 )
( Leftrightarrow 2(1+frac{x}{10})frac{y}{100}+frac{y^2}{10000} leqslant 2-(1+frac{x}{10})^2 )
( Leftrightarrow 2(1+frac{x}{10})frac{y}{100}+frac{y^2}{10000} leqslant 2-(1+frac{2x}{10}+frac{x^2}{100}) )
( Leftrightarrow 2(1+frac{x}{10})frac{y}{100}+frac{y^2}{10000} leqslant 1-(frac{2x}{10}+frac{x^2}{100}) )
( Leftrightarrow 20(10+x)y+y^2 leqslant 100 left [ 100-(20x+x^2) ight ] )
( Leftrightarrow y left [ 20(10+x)+y ight ] leqslant 100 left [ 100-x(20+x) ight ] )
( Leftrightarrow y(20cdot overline{1x}+y) leqslant 100 left [ 100-xcdot overline{2x} ight ] )
( Leftrightarrow y(2cdot overline{1x0}+y) leqslant 100 left [ 100-xcdot overline{2x} ight ] )
( Leftrightarrow ycdot overline{overline{(2cdotoverline{1x})}y} leqslant 100 left [ 100-xcdot overline{2x} ight ] ) (3)
代入 (x=4) 即可求出 (y):
( ycdot overline{28y} leqslant 100 ( 100-4cdot 24 ) ) (4)
我们发现,(3) 式的右侧,出现了与 (2) 式(移项后的一边)相同的部分,这个部分还被乘上了 (100)。而 (3) 式左侧,跟 (2) 式左侧形式相同,都是 未知数 乘以 已得到结果序列的两倍在末尾处添上这个未知数(即帖子中所说「多位数的位数是已开方位数加 1」)。现在,其实已经可以归纳出规律,描述出一个完整的算法了。
但是,这时有些人就会不服:
**,这些破烂式子,都 ** 什么意思啊?*** 为什么要把已得到的结果翻一倍啊?把上一步的不等式两边作差,再乘以 100, 又 ** 是搞什么飞机?
对于这个开方法来说,如果只用代数去推导,确实会让人一头雾水。但是,一但用几何的方法直观地说明一下,这些步骤的意义就会非常明显。看了下面这个几何说明之后,你就会发现,这些看似「无厘头」的步骤,其实都是天经地义的。
看一下这张图(完全平方公式在正数情况下的几何证明):
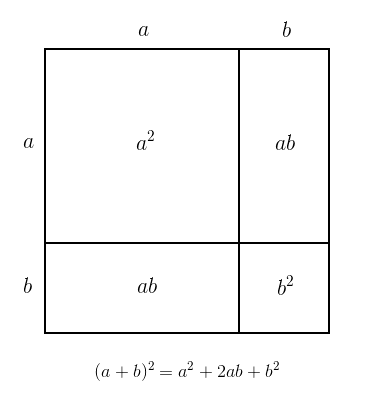
(来源:原创 / Public Domain)
再看看这张图:

(来源:Wikipedia)
发现什么了吗?
刚才计算 (sqrt{2}) 近似值的百分位的过程,实际上就是在这个面积为 (2) 的绿色大正方形中,割出一块边长为 ( overline{1.4x} ; (x=0,;1,;2,;cdots 9) ) 的小正方形,使 (x) 最大。而这个小正方形又可以被两条互相垂直的线切成四个部分。其中一个是边长为己经算出来的部分(精确到上一位的结果,即 (1.4))的正方形(蓝色),剩下的是两个矩形(橙色)和一个正方形(粉色)。
整个小正方形的边长是 ( overline{1.4x} ), 蓝色正方形的边长为 (1.4), 所以橙色矩形的宽就是 ( xcdot 10^{-2} ), 长就是 (1.4), 粉色正方形的边长就是 ( xcdot 10^{-2} ).
现在我们要求这个百分位,实际上就是要让小正方形在大小不超过大正方形的前提下,边长(面积)达到最大。怎么保证面积不超过大正方形呢?我们从大正方形的面积中减去蓝色正方形的面积,使两个橙色矩形和粉色正方形的面积和不超过这个面积差即可,即:
( 2S_{orange}+S_{pink} leqslant S_{green} - S_{blue} )
代入它们的值,可得:
( 2 imes 1.4 cdot (x cdot 10^{-2}) + (x cdot 10^{-2})^2 leqslant 2-1.4^2 )
( Leftrightarrow 2 imes 1.4 cdot (x cdot 10^{-2}) + x^2 cdot 10^{-4} leqslant 2-1.4^2 )
( Leftrightarrow 2 imes 1.4 cdot (x cdot 10^2) + x^2 leqslant 10^4(2-1.4^2) )
( Leftrightarrow 20 imes 14 x + x^2 leqslant 10^4(2-(1+0.4)^2) )
( Leftrightarrow x(280 + x) leqslant 10^4(2-(1+0.8+0.16)) )
( Leftrightarrow x cdot overline{28x} leqslant 10^4(1-0.96) )
( Leftrightarrow x cdot overline{28x} leqslant 10^4(1-0.96) )
( Leftrightarrow x cdot overline{28x} leqslant 100 imes (100-96) )
跟 (4) 式是不是完全一样?所以,这样一解释,那些步骤的意义就很明显了:
- 把 上次的结果 翻一倍,相当于是在求 两个 橙色矩形 的面积。在 ( 20x+x^2 leqslant 100 Leftrightarrow x(20+x) leqslant 100 ) 这个式子中,(20x) 就相当于橙色部分,(x^2) 就相当于粉色部分
- 那个作差操作,相当于从总面积中扣除蓝色的已求部分;再往下算就是再从中扣掉精度提升后蓝色已求部分增加的面积。
- 乘以 100 是因为新的一位比上一位降低了一个数量级,多出来的那三块面积就少了两个数量级。
现在,我们就以计算 ( sqrt{3} )、( sqrt{65536} ) 和 ( sqrt{frac{1}{3}} ) 为例,完整地描述一下这个算法。
例 1 计算 ( sqrt{3} ), 精确到百分位。
首先,在纸上像这样写出被开方数(被开方数的两位对应结果的一位):

找到结果最高位的值(即,求最大的一位数 (x), 使 ( x^2 leqslant 3 )),写在横线上的对应位置上:

把 (x^2) 写到这一位下面,像做除法那样画道横线,作个差:

把后面两位的一组数拽下来补到刚算出的差后面:
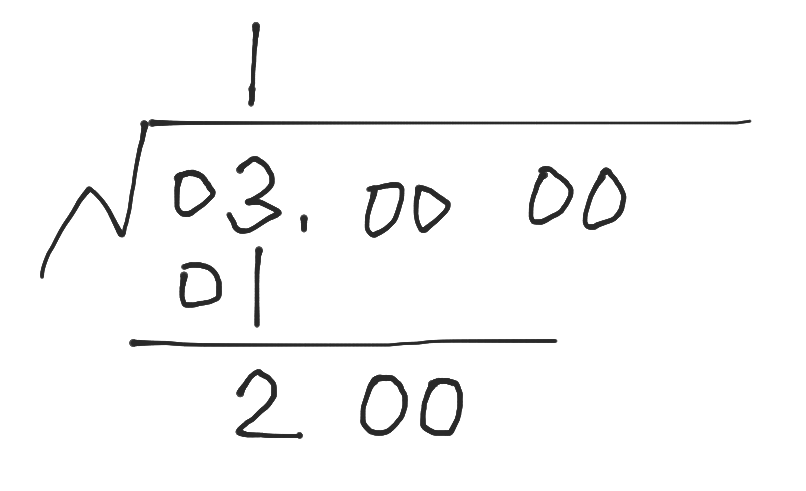
把已经算出的结果翻倍(如果有小数点的话,还要去掉小数点),写在一旁:

前面添上一条横线和一个乘号,后面添上一条横线和一个小于等于号,得到一个不等式:

在每条横线上填一个尽量大的一位数(两条横线上是同一个数),同时保证不等式成立:
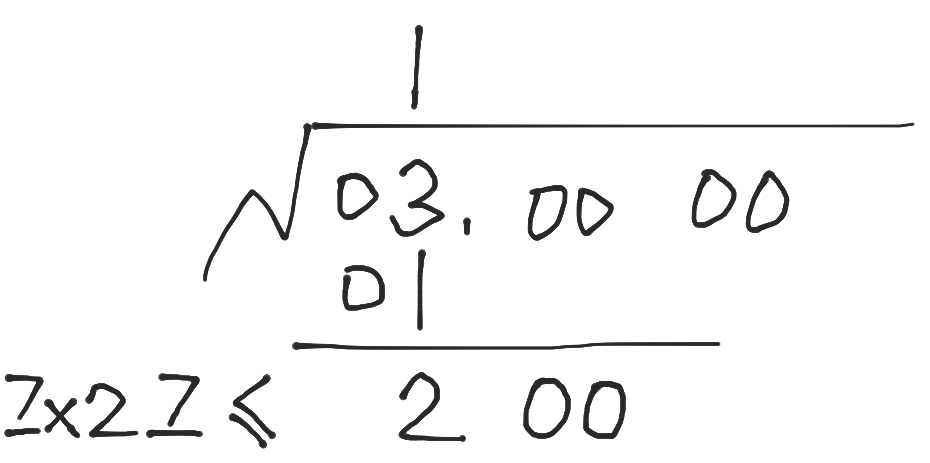
把这个一位数写在上面作为结果:

把乘法的结果写在下面(7×27=189),继续作差:

重复上述过程,直到达到所需精度:
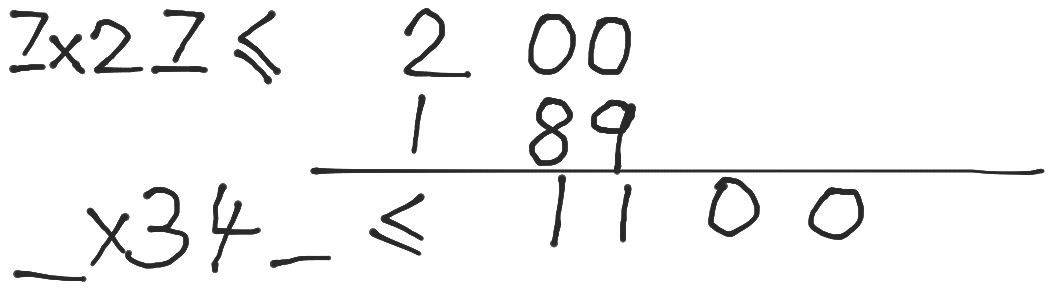
……

例 2 计算 ( sqrt{65536} ).

与例 1 不同的是,这次最后一个不等式是正好取得等号的。取得等号,就说明得数已经是精确结果,不用再往下算了。
例 3 计算 (sqrt{frac{1}{3}}), 精确到千分位。
先把 (frac{1}{3}) 转换为无限小数 (0.333cdots),再开方:

就跟帖子里说的一样,对无限小数开方,运算量不会增大(跟有限小数的计算步骤是完全一样的)。