(图片来源:《天文算法》)
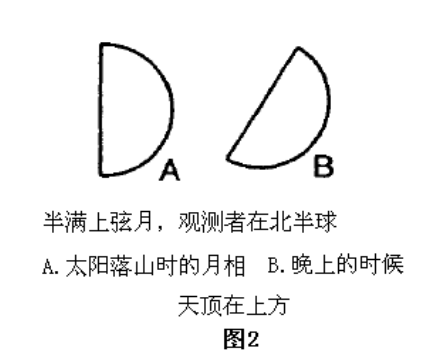
何谓「视差角」?视差角就是天体所在赤道经线和天体所在地平经线之间的夹角,中天之前为负,中天之后为正。就上弦月来说,视差角就是它「倒下」的度数:
(图片来源:《天文算法》)
(注:其实这个例子不大妥当,毕竟黄道经线跟赤道经线的偏差虽然不算太大,但也是有的。不过这个例子是真心很直观,很能说明问题。)
那么怎么计算这个角呢?《天文算法》一书给出了一个公式:
( an{q} = frac{sin{t}}{ an{varphi}cos{delta}-cos{t}sin{delta}} )
(其中 (q) 为天体的视差角,(t) 为天体的时角,( delta ) 为天体的赤纬,( varphi ) 为当地纬度(北纬为正))
但是书上没有推导过程。在这里我们把推导过程补上(以北半球为例):

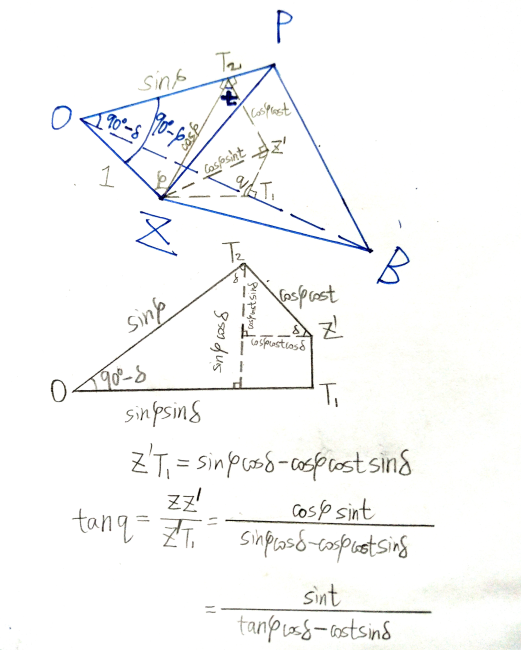
如图,画出天球、地平面、天赤道、平行圈。设天球中心为 (O), 北天极为 (P), 天顶为 (Z), 天体为 (B).
作球面三角形 (BPZ), 在该球面三角形内,所求角 (q) 即 ( angle{ZBP} ). 由时角的定义易知 ( angle{ZPB} = t ).
过 (B)、(P) 作大圆弧 (BP) 交天赤道于 (B'). 易知弧 (BP = {90}^{circ}-delta).
由当地纬度为 (varphi) 易知,弧 ( ZP = {90}^{circ}-varphi ).

现在,我们已经知道球面三角形 (BPZ) 的两边及其夹角,问题是怎么求另一个角。这就比较麻烦。可以先用余弦定理求第三边,然后用正弦定理求出所求角,不过这样一定会算崩。还是把三面角拿出来一步一步推吧:
如下图,过 (Z) 作 (ZZ') 垂直于平面 (POB), 垂足为 (Z'). 过 (Z') 作 (Z'T_1) 交 (BP) 于 (T_1), 过 (Z') 作 (Z'T_2) 交 (OP) 于 (T_2). 连接 (ZT_1), (ZT_2).
跟据球面三角形内角的定义可知 (angle{ZT_2Z'} = angle{P} = t), ( angle{ZT_1Z'} = angle{B} = q ).
这样所有的已知量和未知量就都出现在图上了。接下来从 (OZ=1) 开始一步步求出线段 (ZZ') 和 (Z'T_1) 的长度,再作比求出 ( an{q} ), 就可以得到上文的公式了。这个过程已经写在图里,就不再赘述了。
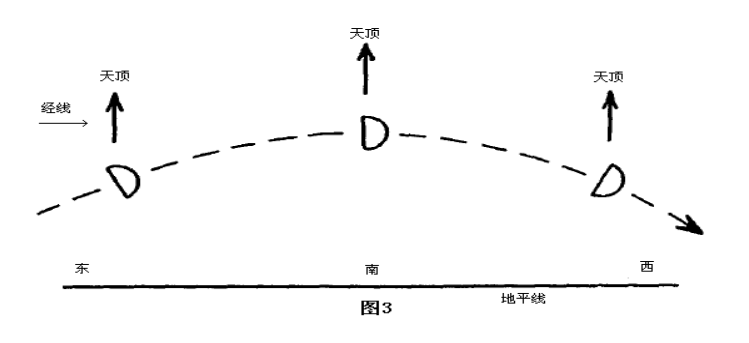
当天体 升/降 时,(大圆)弧 (ZB = {90}^{circ} ), 球面三角形 (ZBP) 三边均已知,直接套用余弦定理得:
( cos{ZP} = cos{BZ}cos{BP} + sin{BZ}sin{BP}cos{angle{ZBP}} )
( cos{({90}^{circ}-varphi)} = cos{{90}^{circ}}cos{({90}^{circ}-delta)} + sin{{90}^{circ}}sin{({90}^{circ}-delta)}cos{q} )
( sin{varphi} = cos{delta}cos{q} )
( cos{q} = frac{sin{varphi}}{cos{delta}} )
在这种情况下,就不需要知道时角 (t).(换句话说,升/降 时的时角是可以算出来的。)