
题意:给你n个兵器,每个兵器有两个攻击力,但只能使用一次,即调用其中一个攻击力,现在你面对了一个老怪,你对它攻击的攻击力只能从1开始,并依此递增1,现在问你你最多能打这个老怪几次。
思路:
思路一:其实这道题上来第一眼想到的是dfs,虽然后来也看到有写dfs的正解,但由于蒟蒻的想法太过于暴力,只水到了50分= =
刚开始的思路很简单,就是用vector存贮输入的每一个值的大小和分组,在dfs时跑过的组直接略过,直到不能再取出最大值或所有组都跑过时,记录一下当前情况下的最大值,并与当前答案比较,输出最大即可。

1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 #include<vector> 5 #include<map> 6 using namespace std; 7 const int N=1e6+10; 8 vector<pair<int,int> >edge[N];//存大小和分组 9 int vis[N],ans;//记录当前组是否来过和答案 10 int dfs(int x,int score){ 11 for(int i=0;i<edge[x].size();++i){ 12 if(vis[edge[x][i].second]) continue; 13 vis[edge[x][i].second]=true; //当前情况处理为来过 14 dfs(x+1,score+1); 15 vis[edge[x][i].second]=false;//当前情况递归结束,还原 16 } 17 ans=max(ans,score);//比较答案 18 } 19 int main(){ 20 int n; 21 scanf("%d",&n); 22 for(int i=1;i<=n;++i){ 23 int x,y; 24 scanf("%d%d",&x,&y); 25 edge[x].push_back(make_pair(x,i));//记录大小及编号 26 edge[y].push_back(make_pair(y,i)); 27 } 28 dfs(1,1); 29 printf("%d ",ans-1); 30 return 0; 31 }
思路二:BFS,我们将每个输入武器的属性之间连一条边,在建好图后就形成了若干个联通块,我们拿样例来举个例子。
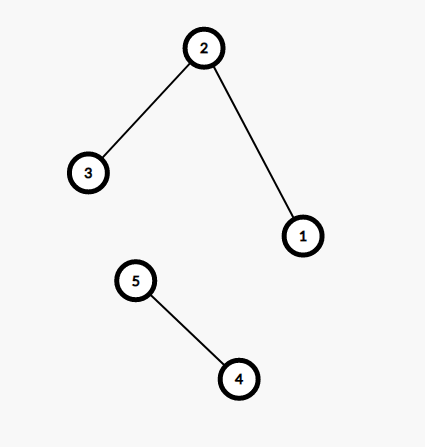
按照题目要求,每对属性都只能选用一个属性值,即一条边上我们只能利用一个节点,我们可以假设每个边上有一个小球,最后每个小球都要待在它所在边的一个节点上,如果我们形成的图没有环(即树),那么这个联通块的边数一定是比点数少1的,也就是说最后一定有一个节点上没有小球,即一个节点没有备选。我们想要从1开始不间断到最后,那么我们肯定要让联通块上权值最大的节点上没有小球,即不选权值最大的点。如果联通块内有环就好说了,因为此时边数一定是大于等于点数的,几个小球可能都要抢节点,就肯定不会有空余的点剩余了。我们要做的就是在每个联通块内bfs,统计是否有环,有的话该联通块内的值都能取,找到最大值直接遍历下一块即可。如果没有环,找到联通块内最大值,答案也就到此为止了。
上代码:

1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 #include<vector> 5 #include<queue> 6 #include<map> 7 using namespace std; 8 const int N=1e6+10; 9 vector<int>edge[N];//这里偷个懒,向量存图好写(/滑稽) 10 int vis[N],rank[N];//rank记录该节点是不是在这个图(该图是树)内的最大值,不是树直接略过 11 bool bfs(int x){ 12 if(!vis[x]){ 13 vis[x]=1; 14 int sum_point=0,sum_edge=0,max_point=x;//点数,边数,权值最大值 15 queue<int>q; 16 q.push(x); 17 while(!q.empty()){ 18 int u=q.front();q.pop(); 19 max_point=max(max_point,u); 20 sum_point++; 21 for(int i=0;i<edge[u].size();++i){ 22 int v=edge[u][i]; 23 sum_edge++; 24 if(!vis[v]) vis[v]=1,q.push(v); 25 } 26 } 27 sum_edge>>=1;//双向边,要除2 28 if(sum_point>sum_edge) rank[max_point]=1; //是树的情况 29 } 30 return (!rank[x]);//看看是不是到此为止了 31 } 32 int main(){ 33 int n; 34 scanf("%d",&n); 35 for(int i=1;i<=n;++i){ 36 int x,y; 37 scanf("%d%d",&x,&y); 38 edge[x].push_back(y);//建图 39 edge[y].push_back(x); 40 } 41 int ans=1; 42 while((vis[ans]&&!rank[ans])||bfs(ans)) ans++; //统计当前ans的rank是不是1 43 printf("%d ",ans-1);//出循环时rank[ans]=0,ans要减1 44 return 0; 45 }
思路三:网上好多大佬都说要用二分图+匈牙利算法,然鹅我连二分图是啥都还不知道。。。
翻阅lyd的书,对二分图做出如下定义:如果一张无向图的N个节点(N>=2)可以分为A,B两个非空集合,其中A和B没有交集,并且在同一集合内的点之间都没有边相连,那么就称这张无向图为一张二分图,A和B分别为二分图的左部和右部.
想要做出这道题,我们还需要明确一些概念:
对于任意一组匹配S(S是一个边集),则属于S的边被称为匹配边,不属于的称为非匹配边,
匹配边的端点被称为匹配点,其余点被称为非匹配点。如果二分图上存在一条链接两个非匹配点的路径,使得非匹配边和匹配边交错出现,那么这条路径就叫匹配S做增广路(划重点)。一条增广路的两端的边一定是非匹配边,且非匹配边数比匹配边数大一(因为交错出现,匹配边被夹在中间),那么我们将S上的所有边的状态取反,则新集合S`还是一组匹配,且匹配上的匹配边数增加了1。那么,二分图的最大匹配S,一定不存在S的增广路.
关于匈牙利算法,强烈推荐大家看一下下面的博客,写得十分有意思:
https://blog.csdn.net/dark_scope/article/details/8880547
如果你看懂了上面的东西,那么恭喜你,你可以用二分图来做这道题了。
由于我们一条边的属性只能用一个,且要求求出最大上升的长度,我们建把武器编号和属性作为建立二分图的标准,跑一遍匈牙利算法就行了,板子和解析在上面的博客里有,这里就不再说了。
最后一点,memset vis数组会导致TLE,所以改用时间戳优化,如果当前的vis(代码中用book记录)值正好等于当前的now值,则在当前情况下处理过,反之则没有。
上代码:

1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 #include<vector> 5 #include<queue> 6 #include<map> 7 using namespace std; 8 const int N=1e6+10; 9 struct Node{ 10 int next,to; 11 }edge[N<<1]; 12 int Head[N],tot,now; 13 void Add(int x,int y){ //建边 14 edge[++tot].to=y; 15 edge[tot].next=Head[x]; 16 Head[x]=tot; 17 } 18 int match[N],book[N];//match表示是否已有匹配和匹配的编号,book是时间戳优化 19 bool find(int x){ //匈牙利算法板子 20 for(int i=Head[x];i;i=edge[i].next){ 21 int v=edge[i].to; 22 if(book[v]!=now){ 23 book[v]=now; 24 if(!match[v]||find(match[v])){ 25 match[v]=x; 26 return true; 27 } 28 } 29 } 30 return false; 31 } 32 int main(){ 33 int n; 34 scanf("%d",&n); 35 for(int i=1;i<=n;++i){ 36 int x,y; 37 scanf("%d%d",&x,&y); 38 Add(x,i);Add(y,i);//编号和属性建图 39 } 40 for(int i=1;i<N;++i){ //寻找答案 41 ++now; 42 if(!find(i)){ 43 printf("%d ",i-1); 44 return 0; 45 } 46 } 47 return 0; 48 }
