题目描述:


题意:给你一张图,再给你几对边,问这几对边想要互达必须经过的的点有多少。
思路分析:其实之前lin大佬讲过一道类似的题压力,题意都差不多,只是那道题问的是每个点被当做必经点的次数。而这道题问的是每对边必经点的数量。既然已经和之前做的一道题联系了起来,就当然要用到那道题的方法了,我们在原图的基础上建一个圆方树,再对每对点跑LCA就可以了,现在的问题是,有了lca后应该如何统计答案,我们要的只是从lca分别到两个点(设为x,y)的路径上的圆点的数量,但lca初始化过程中初始化出来的depth数组同时记录了圆点和方点的数量,其实我们只需将depth[x]和depth[y]的和减去2倍的depth[lca]再除以二向下取证就行了,因为为在路径上圆点和方点一定是交错出现的,以样例为例:
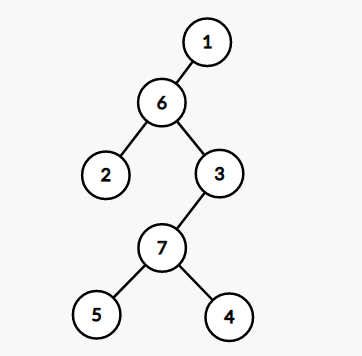
在图中6,7号为方点,其余为圆点,假设我们想求2,4间必通点的数量,depth[2]=3,depth[4]=5,depth[lca]=depth[6]=2;则答案为(3+5-2*2)/2-1=1。
之后就是要注意题目中最后给的是边,我们将每条边两个点四种情况分别求一遍,取一个最大值即可。
这道题调试比较恶心,但想出思路后应该就比较简单了。
上代码:

1 #include<cstdio> 2 #include<algorithm> 3 #include<cstring> 4 #include<stack> 5 #include<vector> 6 using namespace std; 7 const int N=1e5+10; 8 vector<int>edge1[N];//用向量存两个图 9 vector<int>edge2[N]; 10 int dfn[N],low[N],dfn_cnt,scc_cnt,a[N],b[N]; 11 stack<int>sta; 12 int n,m; 13 void tarjan(int x,int fa){ //建圆方图部分 14 low[x]=dfn[x]=++dfn_cnt; 15 sta.push(x); 16 for(int i=0;i<edge1[x].size();++i){ 17 int v=edge1[x][i]; 18 if(!dfn[v]){ 19 tarjan(v,x); 20 low[x]=min(low[x],low[v]); 21 if(low[v]>=dfn[x]){ 22 scc_cnt++; 23 int a; 24 do{ 25 a=sta.top(); 26 sta.pop(); 27 edge2[a].push_back(scc_cnt); 28 edge2[scc_cnt].push_back(a); 29 }while(a!=v); 30 edge2[x].push_back(scc_cnt); 31 edge2[scc_cnt].push_back(x); 32 } 33 } 34 else if(v!=fa) 35 low[x]=min(low[x],dfn[v]); 36 } 37 } 38 int p[N][21],fa[N],depth[N]; 39 void dfs(int x,int pa){ //求LCA部分 40 p[x][0]=fa[x]; 41 depth[x]=depth[fa[x]]+1; 42 for(int j=0;p[x][j]!=0;++j) 43 p[x][j+1]=p[p[x][j]][j]; 44 for(int i=0;i<edge2[x].size();++i){ 45 int v=edge2[x][i]; 46 if(v==pa) continue; 47 fa[v]=x; 48 dfs(v,x); 49 } 50 } 51 int lca(int u,int v){ 52 if(depth[u]<depth[v]) swap(u,v); 53 int d=depth[u]-depth[v]; 54 for(int j=0;d;d>>=1,j++){ 55 if(d&1) u=p[u][j]; 56 } 57 if(u==v) return v; 58 for(int j=20;~j;--j){ 59 if(p[u][j]!=p[v][j]){ 60 u=p[u][j];v=p[v][j]; 61 } 62 } 63 return fa[u]; 64 } 65 void Init(int n){ //多组数据初始化 66 dfn_cnt=scc_cnt=0; 67 for(int i=1;i<=n*2;++i){ 68 edge1[i].clear(); 69 edge2[i].clear(); 70 } 71 memset(p,0,sizeof(p)); 72 memset(depth,0,sizeof(depth)); 73 memset(fa,0,sizeof(fa)); 74 memset(dfn,0,sizeof(dfn)); 75 memset(low,0,sizeof(low)); 76 while(!sta.empty()) sta.pop(); 77 } 78 int cal(int x,int y){ 79 if(x==y) return 0; 80 return (depth[x]+depth[y]-2*depth[lca(x,y)])/2-1; 81 } 82 int main(){ 83 //freopen("in.txt","r",stdin); 84 while(scanf("%d%d",&n,&m)==2&&n&&m){ 85 Init(n); 86 scc_cnt=n; 87 for(int i=1;i<=m;++i){ 88 int x,y; 89 scanf("%d%d",&x,&y); 90 a[i]=x;b[i]=y; //存每条边上的点,之后要用到 91 edge1[x].push_back(y); 92 edge1[y].push_back(x); 93 } 94 for(int i=1;i<=n;++i) //注意图可能不连通 95 if(!dfn[i]) 96 tarjan(i,-1); 97 for(int i=1;i<=scc_cnt;++i) 98 if(!depth[i]) dfs(i,-1); 99 int t; 100 scanf("%d",&t); 101 while(t--){ 102 int x,y; 103 int ans=0; 104 scanf("%d%d",&x,&y);//计算答案 105 ans=max(max(cal(a[x],b[x]),cal(a[x],b[y])),max(cal(a[y],b[x]),cal(a[y],b[y]))); 106 printf("%d ",ans); 107 } 108 } 109 return 0; 110 }
