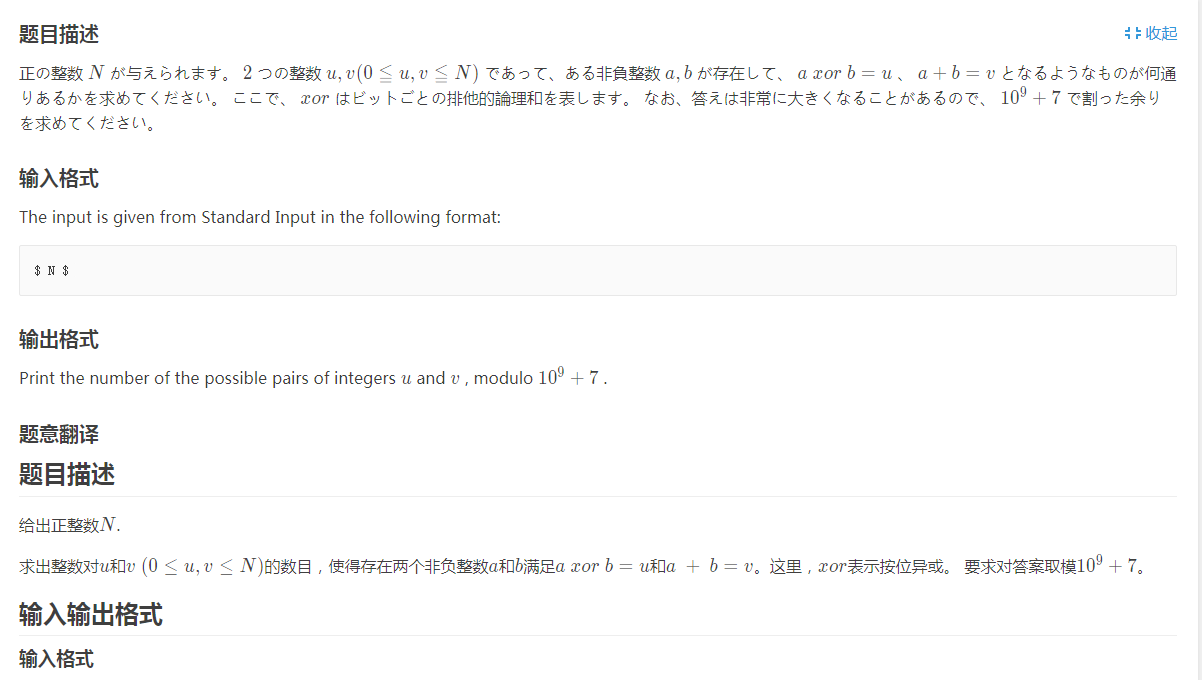


题意:给定一个n,求存在0<=u,v<=n,使得有a,b满足a^b=u,a+b=v的对数,对1e9+7取模。
思路分析:本来看到这道题题意以为是和前几天做的一道位或的题类似,后来想想不一样,毕竟那道题没让你输出方案数,输出最大结果就行。
后来发现这其实是一个找规律,我们可以先手算出前几个值,就会发现他们其实是存在着关系的,第x个数满足d[x]=d[x/2]+d[(x-1)/2]+d[(x-2)/2]。
当然洛谷上的神犇给出了一种理解,但是蒟蒻太弱了不怎么看得懂,放在这里供大家看一下吧。QAQ

最后上代码:

1 #include<cstdio> 2 #include<algorithm> 3 #include<cstring> 4 #include<map> 5 using namespace std; 6 map<int,int>num; 7 typedef long long ll; 8 const int N=1e6+10; 9 const int Mod=1e9+7; 10 ll cal(ll x){ 11 if(num[x]!=0) return num[x]; 12 return num[x]=(cal(x/2)+cal((x-1)/2)+cal((x-2)/2))%Mod; 13 } 14 int main(){ 15 num[0]=1;num[1]=2; 16 ll n; 17 scanf("%lld",&n); 18 printf("%lld ",cal(n)); 19 return 0; 20 }
