3D点云特征描述与提取是点云信息处理中最基础也是最关键的一部分,点云的识别。分割,重采样,配准曲面重建等处理大部分算法,都严重依赖特征描述与提取的结果。从尺度上来分,一般分为局部特征的描述和全局特征的描述,例如局部的法线等几何形状特征的描述,全局的拓朴特征的描述,都属于3D点云特征描述与提取的范畴,
特征描述与提取相关的概念与算法
1.3D形状内容描述子(3D shape contexts)
利用描述子建立曲面间的对应点在3D物体识别领域有广发的应用,采用一个向量描述曲面上指定点及邻域的形状特征,通过匹配向量的值来建立不同曲面点的对应关系,此相邻则则称为指定点的俄描述子,经典描述子的3D形状内容描述子结构简单,辨别力强,且对噪声不敏感,
2,旋转图像(spin iamge)
旋转图像最早是由johnson提出的特征描述子,主要用于3D场景中的曲面匹配和模型识别,
3,涉及的算法相关的资料
3D形状内容描述子
https://en.wikipedia.org/wiki/Shape_context
www.eecs.berkeley.edu/Research/Projects/CS/vision/shape/belongie-pami02.pdf
还有很多中描述子的理论与算法的研究,不再一一列出来
关于理论的部分有待研究,但是暂时我只是学习会用。
关于PCL中特征描述与提取模块和相关类的介绍
Classes |
|
| class | pcl::ShapeContext3DEstimation< PointInT, PointNT, PointOutT > |
| 实现3D形状内容描述子算法 | |
| class | pcl::BOARDLocalReferenceFrameEstimation< PointInT, PointNT, PointOutT > |
| 实现局部坐标系估计的方法 特别是处理点云边缘或有孔洞有特殊的处理方式 | |
| class | pcl::BoundaryEstimation< PointInT, PointNT, PointOutT > |
| 实现估计一组点集是否处于指定点的投影区域的边缘位置 | |
| class | pcl::CRHEstimation< PointInT, PointNT, PointOutT > |
| 实现摄像头旋转直方图描述子,利用概算法主要进行刚体对象的位姿估计 | |
| class | pcl::CVFHEstimation< PointInT, PointNT, PointOutT > |
| 实现聚类视点直方图CVFH描述子的计算 主要是针对解决有残缺的点云识别问题 | |
| class | pcl::ESFEstimation< PointInT, PointOutT > |
| 实现ESF描述子,主要用于实时对三维场景中的点云模型进行分类而提出的 | |
| class | pcl::Feature< PointInT, PointOutT > 是所有特征相关模块中其他类的基类 |
| class | pcl::FeatureWithLocalReferenceFrames< PointInT, PointRFT > |
| 实现FPFH描述子算法主要针对点云配准过程中对应点而提出的 |
|
(关于他的类还有很多可以直接去网站自己查看)
PCL中描述三维特征相关基础
理论基础
在原始表示形式下,点的定义是用笛卡尔坐标系坐标 x, y, z 相对于一个给定的原点来简单表示的三维映射系统的概念,假定坐标系的原点不随着时间而改变,这里有两个点p1和p2分别在时间t1和t2捕获,有着相同的坐标,对这两个点作比较其实是属于不适定问题(ill—posed problem),因为虽然相对于一些距离测度它们是相等的,但是它们取样于完全不同的表面,因此当把它们和临近的其他环境中点放在一起时,它们表达着完全不同的信息,这是因为在t1和t2之间局部环境有可能发生改变。一些获取设备也许能够提供取样点的额外数据,例如强度或表面反射率等,甚至颜色,然而那并不能完全解决问题,单从两个点之间来 对比仍然是不适定问题。由于各种不同需求需要进行对比以便能够区分曲面空间的分布情况,应用软件要求更好的特征度量方式,因此作为一个单一实体的三维点概念和笛卡尔坐标系被淘汰了,出现了一个新的概念取而代之:局部描述子(locl descriptor)。文献中对这一概念的描述有许多种不同的命名,如:形状描述子(shape descriptors)或几何特征(geometric features),文本中剩余部分都统称为点特征表示。通过包括周围的领域,特征描述子能够表征采样表面的几何 性质,它有助于解决不适定的对比问题,理想情况下相同或相似表面上的点的特征值将非常相似(相对特定度量准则),而不同表面上的点的特征描述子将有明显差异。下面几个条件,通过能否获得相同的局部表面特征值,可以判定点特征表示方式的优劣:
(1) 刚体变换-----即三维旋转和三维平移变化 不会影响特征向量F估计,即特征向量具有平移选转不变性。
(2) 改变采样密度-----原则上,一个局部表面小块的采样密度无论是大还是小,都应该有相同的特征向量值,即特征向量具有抗密度干扰性。
(3) 噪声---数据中有轻微噪声的情况下,点特征表示在它的特征向量中必须保持相同或者极其相似的值,即特征向量对点云噪声具有稳定性。
通常,PCL中特征向量利用快速kd-tree查询 ,使用近似法来计算查询点的最近邻元素,通常有两种查询类型:K邻域查询,半径搜索两中方法
法线估计实例
一旦确定邻域以后,查询点的邻域点可以用来估计一个局部特征描述子,它用查询点周围领域点描述采样面的几何特征,描述几何表面图形的一个重要属性,首先是推断它在坐标系中的方位,也就是估计他的法线,表面法线是表面的一个重要的属性,在许多领域都有重要的应用,如果用光源来生成符合视觉效果的渲染等,
代码解析:normal_estimation.cpp
(实现对输入点云数据集中的点估计一组表面法线)执行的操作是:对应点云P中每一个点p得到p点最近邻元素,计算p点的表面的法线N,检查N的方向是否指向视点如果不是则翻转。
视点默认坐标是(0,0,0)可使用setViewPoint(float vpx,float vpy,float vpz)来更换
#include <pcl/io/io.h> #include <pcl/io/pcd_io.h> #include <pcl/features/integral_image_normal.h> //法线估计类头文件 #include <pcl/visualization/cloud_viewer.h> #include <pcl/point_types.h> #include <pcl/features/normal_3d.h> int main () { //打开点云代码 pcl::PointCloud<pcl::PointXYZ>::Ptr cloud (new pcl::PointCloud<pcl::PointXYZ>); pcl::io::loadPCDFile ("table_scene_lms400.pcd", *cloud); //创建法线估计估计向量 pcl::NormalEstimation<pcl::PointXYZ, pcl::Normal> ne; ne.setInputCloud (cloud); //创建一个空的KdTree对象,并把它传递给法线估计向量 //基于给出的输入数据集,KdTree将被建立 pcl::search::KdTree<pcl::PointXYZ>::Ptr tree (new pcl::search::KdTree<pcl::PointXYZ> ()); ne.setSearchMethod (tree); //存储输出数据 pcl::PointCloud<pcl::Normal>::Ptr cloud_normals (new pcl::PointCloud<pcl::Normal>); //使用半径在查询点周围3厘米范围内的所有临近元素 ne.setRadiusSearch (0.03); //计算特征值 ne.compute (*cloud_normals); // cloud_normals->points.size ()应该与input cloud_downsampled->points.size ()有相同的尺寸 //可视化 pcl::visualization::PCLVisualizer viewer("PCL Viewer"); viewer.setBackgroundColor (0.0, 0.0, 0.0); viewer.addPointCloudNormals<pcl::PointXYZ,pcl::Normal>(cloud, cloud_normals); while (!viewer.wasStopped ()) { viewer.spinOnce (); } return 0; }
运行结果并执行:

(2)估计一个点云的表面法线
表面法线是几何体表面一个十分重要的属性,例如:在进行光照渲染时产生符合可视习惯的效果时需要表面法线的信息才能正常进行,对于一个已经已经知道的几何体表面,根据垂直于点表面的的矢量,因此推推处表面某一点的法线方向比较容易,然而由于我们获取的点云的数据集在真实的物体的表面表现为一组定点的样本,这样就会有两种方法解决:
1 . 使用曲面重建技术,从获取的点云数据中得到采样点对应的曲面,然后从曲面模型中计算出表面法线
2. 直接从点云数据中近似推断表面法线
在确定表面一点法线的问题近似于估计表面的一个相切面法线的问题,因此转换过来就是求一个最小二乘法平面拟合的问题
(3)使用积分图进行法线估计
使用积分图计算一个有序的点云的法线,注意此方法只适用有序点云
代码解析normal_estimation_using_integral_images.cpp
#include <pcl/io/io.h> #include <pcl/io/pcd_io.h> #include <pcl/features/integral_image_normal.h> #include <pcl/visualization/cloud_viewer.h> int main () { //打开点云 pcl::PointCloud<pcl::PointXYZ>::Ptr cloud (new pcl::PointCloud<pcl::PointXYZ>); pcl::io::loadPCDFile ("table_scene_mug_stereo_textured.pcd", *cloud); //创建法线估计向量 pcl::PointCloud<pcl::Normal>::Ptr normals (new pcl::PointCloud<pcl::Normal>); pcl::IntegralImageNormalEstimation<pcl::PointXYZ, pcl::Normal> ne; /**************************************************************************************** 三种法线估计方法 COVARIANCE_MATRIX 模式从具体某个点的局部邻域的协方差矩阵创建9个积分,来计算这个点的法线 AVERAGE_3D_GRADIENT 模式创建6个积分图来计算水平方向和垂直方向的平滑后的三维梯度并使用两个梯度间的向量 积计算法线 AVERAGE_DEPTH——CHANGE 模式只创建了一个单一的积分图,从而平局深度变化计算法线 ********************************************************************************************/ ne.setNormalEstimationMethod (ne.AVERAGE_3D_GRADIENT); //设置法线估计的方式AVERAGE_3D_GRADIENT ne.setMaxDepthChangeFactor(0.02f); //设置深度变化系数 ne.setNormalSmoothingSize(10.0f); //设置法线优化时考虑的邻域的大小 ne.setInputCloud(cloud); //输入的点云 ne.compute(*normals); //计算法线 //可视化 pcl::visualization::PCLVisualizer viewer("PCL Viewer"); //视口的名称 viewer.setBackgroundColor (0.0, 0.0, 0.5); //背景颜色的设置 viewer.addPointCloudNormals<pcl::PointXYZ,pcl::Normal>(cloud, normals); //将法线加入到点云中 while (!viewer.wasStopped ()) { viewer.spinOnce (); } return 0; }
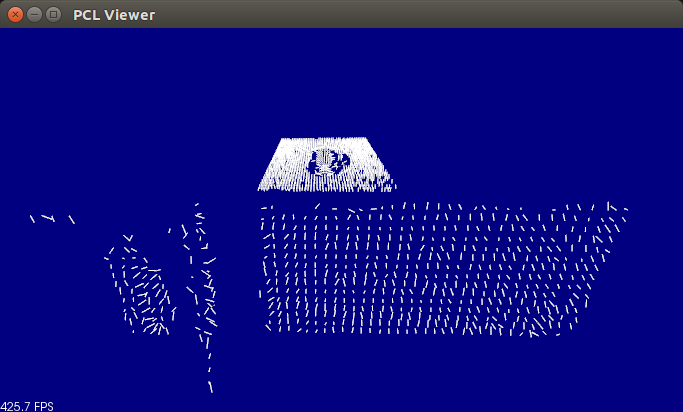
运行结果为:
微信公众号号可扫描二维码一起共同学习交流

未完待续*********************8